ぷよぷよと連想記憶【準備編】
こんばんは、すしくんです。
今回は前回の
scitaku.hatenablog.com
この記事の最後の方で、pottsモデルにぷよのフィールドを連想記憶として埋め込みたいということを言っていたので、今回はそれをやってみました。
連想記憶については前々回の
scitaku.hatenablog.com
これを読むとなんとなくわかると思います。
目次
はじめに
前回言っていた通り、イジングモデルの逆推定問題(連想記憶)を拡張し、pottsモデルのパラメータをデータから逆推定するプログラムを書きました。
学習方程式は、イジングの場合とほとんど変わらなかったので、以下では結果を天下り的に書きます。
また、今回はデータを大量に準備する気力が湧かなかったので予備実験までの結果を載せて終わります。(誰かデータ作ってくれ)
一応学習方程式導出の詳細をアップしておきます。
・計算ノート
プログラムもgitにあげたいと一瞬思ったんですが、あまりに汚いのでやめました()
モデルと学習方程式
まずpottsモデルとはイジングモデルのように0か1だけでなく、0、1、2、…qー1の状態を取れるように拡張したモデルです。
難しく考えなくても、ぷよぷよのように赤ぷよ、青ぷよ、黄ぷよ…と状態を変化させられると考えると良いです。
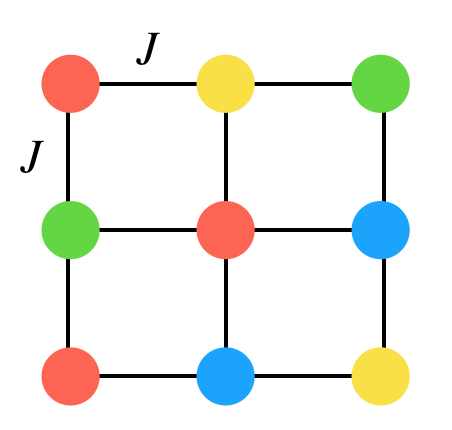
このモデルは上のように、様々な「色ぷよ」状態をとりつつ他の「ぷよ」と相互作用するようなモデルです。
実際のぷよぷよもある点に様々な色のぷよが存在していることからも、このモデルがぷよぷよをよく表現してくれそうという期待が持てます。
また、このモデルでは色ぷよの配置によってエネルギーを定義でき、今回は以下のように設定しました。はあるぷよviとvjが同じ色ならば1、違うならば0となるように定義しています。
は相互作用の強さで、負符号だと相互作用しているぷよと同じ色ぷよになりたがり、正だと違う色になりたがります。
はバイアス項(物理ではゼーマン項と呼ばれます)で、負符号の場合はあるぷよについてある値
に対応した色ぷよにさせようとします。逆に正だと違う色にさせようとする効果があります。
以上を踏まえた上で、このモデルでぷよぷよのフィールドを再現する、というのは例えば階段連鎖を考えてみます。(一部切り抜いたフィールドと思ってください)
として、簡単のため線で繋がれたぷよ同士に相互作用が働くことにしています。そうすると階段連鎖は、マイナス符号がついている組には同じ色ぷよがきて、正符号の相互作用が働くところには違う色が来て欲しくて…となっていることがわかると思います。(J,-Jは一部しか書いていませんが他のところも同様に考えられます)
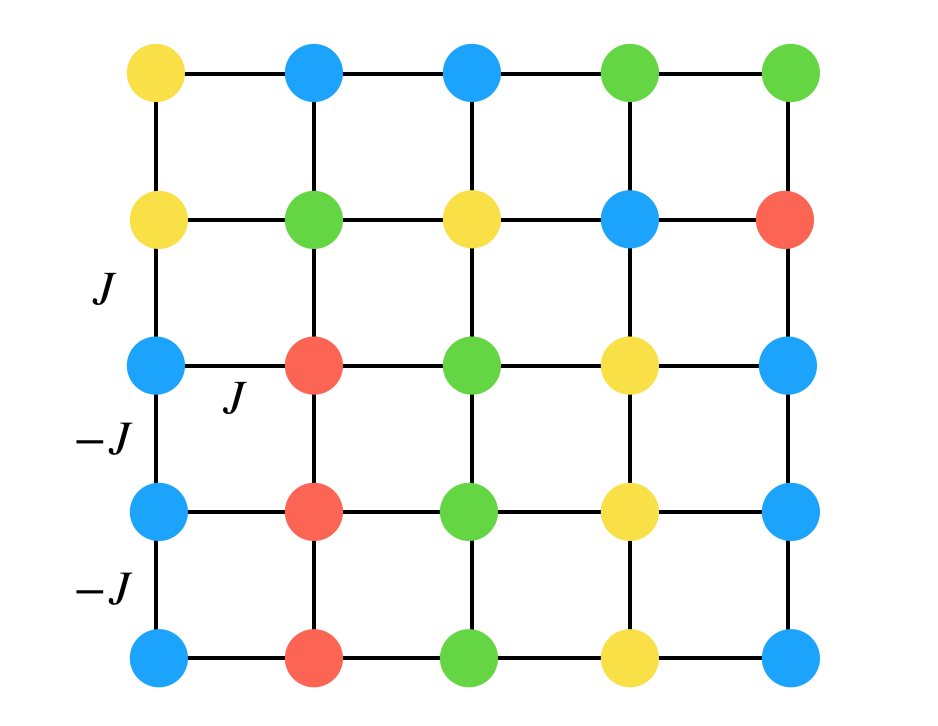
更に遠くのぷよと相互作用する組を考えると、例えばタブーの形にはならないようにパラメータを調整していけることがわかると思います。
このことからわかるように、pottsモデルにおいて「あるフィールドのデータから相互作用の強さと符号を推定し、連鎖において何が大事なのかを推定することが可能ではないか」と思って今回の遊びをはじめました。
また、詳しい人は疑問に思ったかもしれませんが、一般的なボルツマンマシンでは表からは見えない「隠れ変数」というものを導入します。これはeffectiveに3、4、5…体の相互作用を取り入れることができ、非常に強力です。しかし、今回はまずシンプルなモデルから出発したいのと、結果の解釈が難しくなることから採用していません。しかし、多体の効果は連結に対して効率よく損得を考えることができそうなので、いずれやってみたいですね。
さて、本題に戻ります。
pottsモデルの隠れ変数なしの一般的な学習方程式を天下り的に与えると
このようになります、上の式についてはについてそれぞれ別々に考えます。
はモデルから
という(物理)量を計算し、その平均値で近似することができます。
は簡単で、入力したい(学習したい)データ全てに渡り平均をとればすぐに計算ができます。
要するにこの学習方程式は、データのある色がどのくらいあるかの平均(を1ぷよあたりに直したもの)と、モデルから計算される平均値を同じになるようにしなさい、ということです。二つ目は、データとモデルの間のあらゆるぷよ2つの組みの色関係を揃えなさいと言っています。
イメージとしては色ぷよの数だけイジングボルツマンマシンを並べて、それを二つ目の式で繋いでいるといった感じでしょうか?個人的にはが結局イジングになるだけなので本質的には何も変わらないと思っています。(そっちの方が既存の手法が適用できて楽)
しかし、ぷよぷよの計算に以上の方程式を適用する場合、若干の不便さがあります。それは連鎖において「色そのもの」というのはなんの意味もないからです。
実際のフィールドを考えてみると
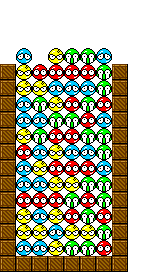

最初の色の並びを"回した"配列は変換の前後でフィールドを等価にします。
この対称性を考慮した上で今回の学習方程式は
今回は何もない空間にも状態を与えているため、0を対応させています。この学習方程式では、ぷよがない空間以外はバイアスが同じ値になり、色ぷよの変換に対する対称性を反映させることができます。
計算
では、具体的に学習方程式から学習がどのように進むかみていきましょう。
コードをあげない代わりにプログラムの流れだけ書いておきます。
- 学習データから
を計算する
- フィールドに適当にぷよを配置する(ぷよが置かれない場合も今回は考慮しています)
- 温度アニーリングを用いながらMCMCの一種であるメトロポリス・ヘイスティングス法でフィールドを低温まで冷やす(その時のパラメータにおけるエネルギーが最小のぷよ配置を求める)
などの(物理)量をサンプリングし、平均値を期待値と近似する。
- パラメータを勾配法を用いて更新する。(
は学習率)
- 更新した後3に戻り訓練回数分繰り返す
今回準備編であるため参考程度ですが、予備実験に用いたハイパーパラメータは(学習率、緩和に用いたMCステップ数、MCサンプリングの回数、最高温度、最低温度、温度点の数、訓練回数)
このようにしました、パラメータの初期値は正規分布で適当に決めています。
温度についてですが、特徴的な温度スケールはせいぜい1オーダーなのと、Jijがランダムに入り混じった系は転移温度が低いため、多分1で十分高温だと思います。
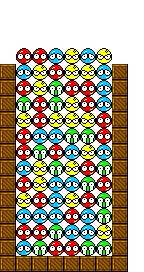
さて、予備実験の結果をみてみましょう。今回はフィールドを2枚だけ記憶させました。(ちなみに左は僕が適当に作ったもので、右はももけんさんのGTRです)


学習回数とパラメータの変化をみてみましょう、本当は全部確認すべき(というかlossとか尤度とかD_KLとか計算したいけどあまりわかってない)なんですが、適当に2つだけ抜き出してます。
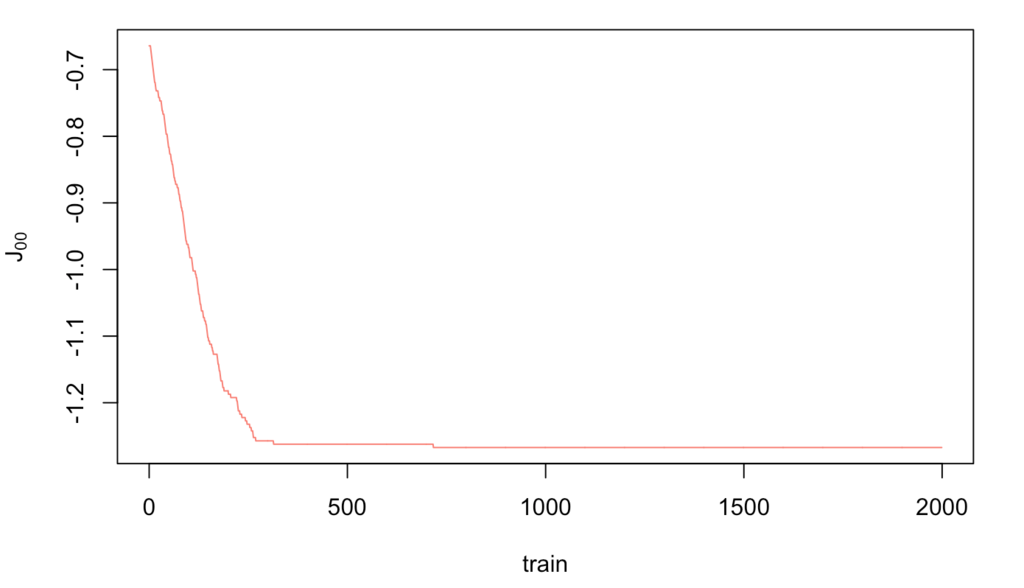
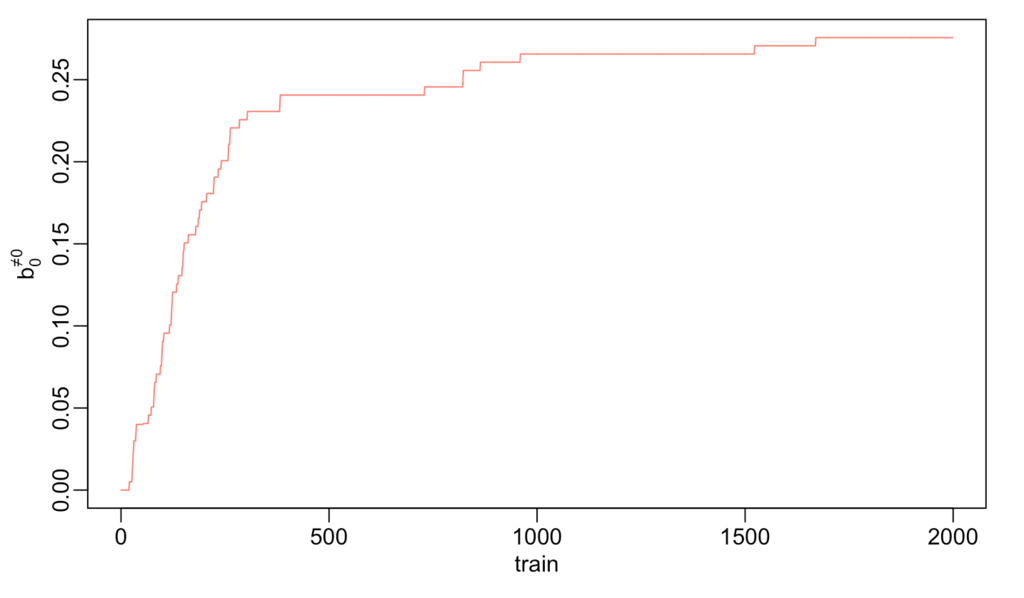
まぁある程度は収束してるから大丈夫かな・・・。
こうして学習が終了した後のパラメータで、MCMCで更新していくと2つの形のうちのどちらかが想起されます。
例えば左のような初期条件から学習済みパラメータで、低温まで冷やしていくと(エネルギーが最小のぷよの配置を求める)最終的には右のような、学習したGTRのうちの一つが出現します。

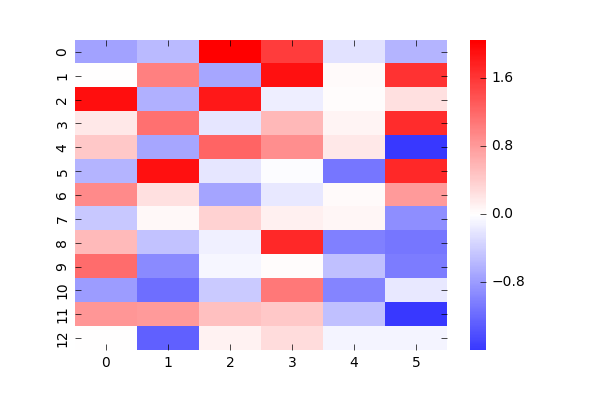
これだけみててもよくわからないので、パラメータについて見ていきましょう。
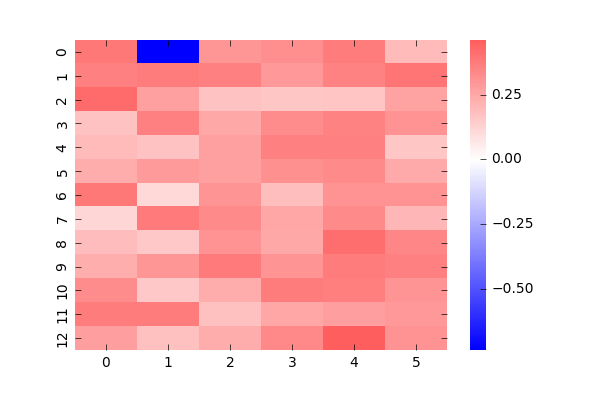
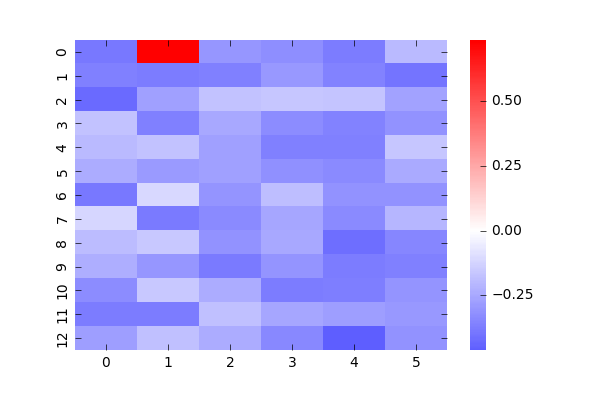
これは、あるぷよに対して他のぷよがどういう値で相互作用しているかの図です。赤は正符号での相互作用(違う色になりたがる)、青は負符号で(同じ色になりたがる)の相互作用で、濃さはその強さを表します。1つのぷよと他のぷよの関係を表しているため、全部載せると78枚になってしまうので適当に2つ持ってきました。(自分自身のところは0としています)
左図は(1,1)のぷよに対する相関でGTRの一番底です。期待としてはGTRの形が青で浮かび上がってくると思ったんですが、そうはなってませんね。おそらくデータが圧倒的に少ないため、他のパラメータで調整しているのだと思います。
右図は(2,11)のデータで、1つ目の学習データでぷよがなかったところです。ここも他に対して全て違う状態になる傾向が少し見えると思いましたが、見えませんでした。
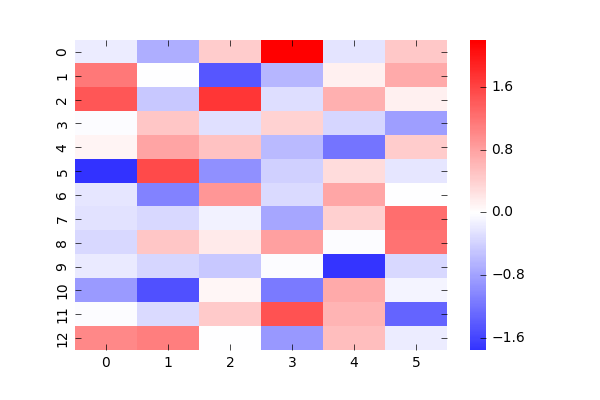
次にバイアスを見て見ましょう、これはと
で分けています。1枚目の学習結果を強く反映しているのがわかります。
今回の軽い計算結果はここまでとします。
次回
今回はデータを集める気力がなかったので、まずは小さなデータで最低限期待されることが実現しているかなどをチェックする形になりました。期待通りのものもそうでなかったものもありますが、どのみちデータが足りないに尽きていると思われます。
次回は大量にデータを用意して学習した結果を報告できたらなぁと思います。
上手くいったら、いいなあ。