ぷよぷよと統計力学
こんばんは、すしです。
なんだか仰々しいタイトルですが、中身は大したことないです。今回は前回(以下リンク)の続きを書いていこうと思います。
scitaku.hatenablog.com
一応前回の記事を読まなくてもわかるように纏めますが、気になる方は読んでみてください。
目次
はじめに
前回はフィールドにぷよぷよをランダムに敷き詰めていったときに、発生する連鎖数の平均値を様々な大きさのフィールドで調べていきました。
結果的には僕たちがプレーしているフィールドを1として、アスペクト比を保ったままの倍率をLとするとその平均連鎖数は程度になることがわかりました。
他にもお邪魔ぷよをフィールドに一定の割合でドープしてみたりしましたが、結局は完全ランダムに配置した時が一番連鎖の平均値が高いという結果でした。
そこで今回は「ぷよの生成過程にあるルールをつけて、ランダム生成の平均連鎖数を超えることができるのか?」というテーマでやっていきたいと思います。
僕たちが普段組んでる連鎖とは一体なんなのか、という問いに何か回答を与えることができたらいいなーくらいの気持ちでやってます。
統計力学の話
最初にあるルールでと書きましたが、今回は僕の専門である「統計力学」の範疇で与えられるルールでぷよをフィールドに生成していきたいと思います。
そこでまずは今回用いる統計力学の知識を簡単にですが纏めていきます。
イジングスピンとベクトルスピン
イジングスピンといえば割と聞いたことがあるという人も多いのではないでしょうか?
機械学習や量子コンピュータの分野で出てきたりするアレです。
元々は電子や陽子が持つ内部自由度で角運動量の次元を持つ物理量ですが、もっと簡単に言うと磁石の最小単位です。

上の図のように、一番基本的なS=1/2ではスピンは上か下のいずれかを向いており、それがマクロに同じ方向に向いていると磁石になります。(上右図)
このように上か下かを向いている矢印を格子状に置いたモデルをイジングスピンモデルと言います。0か1の2状態を取ることからもなんかコンピュータぽくてそれっぽい応用ができそうな感じがしますよね。
量子コンピュータでは、古典的な描像である「上か下」でなく量子的な「上と下の状態の重ね合わせ」が重要になってきますが、今回は全て古典のお話です。
さて、離散的な状態を取るイジングスピンに対して連続的な状態をとるスピンがいても良さそうですよね?それがベクトルスピンモデルと言うもので、XY模型やHeisenberg模型などがそれにあたります。前者は2次元のベクトル(矢印)を扱い、後者は3次元のベクトルを扱います。量子スピンとのつながりでいくとS→∞の極限に対応していて(厳密にはS→∞,h→0,Sh=constの極限)、物質的にはS=5/2あたりから古典描像に近くなると言われています。(うろ覚え)
しかし、今回はあんまり出てこないので忘れていただいて結構です。
ハミルトニアンと自由エネルギー
ここから具体的な話になってきますが、今回のメインであるぷよ生成のルールについて話していきます。
統計力学では(それだけに限りませんが)モデルを動かすルールのことを「ハミルトニアン」と言います。
物理的にはエネルギーを与える関数(量子力学では演算子)ですが、ここではモデルにどういう風になって欲しいのか?を規定しているものだと思ってください。自然界において万物はマクロにはより安定な状態、つまりよりエネルギーが低い状態にいくため、エネルギーの関数を最小にする状態が実現します。統計に明るい人は損失関数だと思うと理解しやすいでしょう。
次に自由エネルギーについてです。ルールを決めているのはハミルトニアンと言いましたが、これは厳密ではありません。より厳密にはモデルの振る舞いはハミルトニアン(エネルギー)とエントロピー*1(乱雑さの指標)で決まります。具体的な表式は以下の通りで、これを最小化する状態が実際には実現します。

T=0ではエネルギーが全ての振る舞いを支配していますが、T≠0ではエントロピーとの競合があるためエネルギーだけでは状態が決まらなくなります。
例えばスピンを2つだけ並べた状況を考えましょう。(ここではより一般的に長さ1のベクトルスピンを考えます)また、エネルギー関数Uは図中のものとします。

まずT=0を考えるとFを最小化するスピンの配置はどうなるでしょう?この状況ではUのみを最小化すれば良いですね、つまり2つのスピンが平行になっている時U=-1となって最小値をとります。

有限温度ではどうでしょうか?T<<1の時、エントロピーが十分に大きな値を取らない場合*2は、U=-1の状態が最小であるためスピンは基本的に平行でいようとします。基本的に、と言うところが重要で有限温度ではエントロピー項があるため、エネルギーで多少損してもこちらで得することが可能になります。要するに二つのスピンが平行な状態から揺らぐ(少しだけ違う方向を向く)ことが可能になるのです。今回のテーマではこの効果が重要な要素の一つになります。

T>>1ではエネルギーを尊重するよりエントロピー項を尊重した方がお得になるため、なるべく乱雑になろうとします。その結果、エネルギーが最大になるスピンが反平行になる状態も実現します。これは身近な例でいくと、水は低温で綺麗な結晶構造を持ちますが(エントロピー低)、高温では気体になって好き勝手に動く(エントロピー高)ことに対応しています。

前回の記事で若干触れましたが、ランダムフィリングの計算ではT→∞(またはU→0)の極限を考えていることに相当しているため、エントロピー(乱雑さ)だけで状態が決まっている状況と解釈することもできます。
ランダムフィリングは任意のハミルトニアンでの温度無限大での計算なので、今回は逆にT=0に近いところを考えていこうというわけです。
自発的対称性の破れ
ここまでの材料があってやっとこの話ができます。自発的対称性の破れと聞くと何年か前にノーベル賞を取られた南部先生のことを思い出す人が多いと思いますが、まさにその話です。(南部先生が受賞された研究領域は素粒子とかについてだったと思いますが、本質的には同じです。)
まず対称性とはなんでしょうか、例えばスピンは何も制限がなければ何処を向いてもいいですよね?

これを連続対称性といいます。ベクトルの成分によりますがのようにかけるスピンなら平面、
なら立体をぐるぐる回ることができます。
しかし、上の例のようにお互いの向きによってエネルギーが変わるような状況を考えると、Tが十分に小さい領域ではエネルギーを尊重します。よって、1つ1つのスピンは好き勝手な方向を向くことができなくなります。「いろんな方向を本来向くことができるにも関わらず、ある特定の方向を向いてしまう」ことを連続対称性*3の破れ、広くは自発的対称性の破れといいます。
温度が高いと無秩序な状態(対称性が高い)でいられますが、温度が十分に低いと秩序的(対称性が低い)な状態へ対称性が破れて変化します、これをもっと一般的な言葉では相転移といいます。

また身近な例である水を取り上げます。例えばまず、気体状態の水は下図のように好きな方向へ動けますよね?*4この状態から温度を下げていくと皆さんご存知のように液体になり個体になります。これもある種の対称性を破って、相転移を起こして物質の状態が変わっている様子が見えていると言うわけです。*5

ポッツモデルとクロックモデル
最後に今回のモデルとして採用したポッツモデル、そしてその仲間のクロックモデルの説明をします。
ポッツモデルとは一言でいえばイジングスピンモデルの拡張です。イジングモデルは上か下かの2つの状態をとるのに対して、こちらのモデルはq個の状態をとります。上でも下でもない状態、のように捉えるとなんだか難しい気になりますが、単純に赤ぷよ黄ぷよ青ぷよ…みたいな状態を考えると想像しやすいと思います。よって今回はこのモデルを用いてぷよぷよをモデル化しました。
次にクロックモデルはXY模型を離散化したものに対応しています。横着して図を使いまわしますが、下図のようにの離散化されたq個の2次元ベクトルの内いずれかをとるモデルになっています。こちらはq→∞の連続極限が自然にXY模型に繋がるため、離散的な性質と連続的な性質を兼ね備えたモデルと言えます。*6
 」
」
こちらのモデルで考える道もありだと思いますが、今回はポッツモデルを採用しました。
今回のお話
導入が長くなってしまいましたが、今回の具体的な内容について説明していきます。
モデルの説明をしてそれぞれの結果について述べていきたいと思います。
ぷよぷよとポッツモデル
導入でも話しましたが、今回はぷよぷよをポッツモデルに落とし込み、解析していきます。
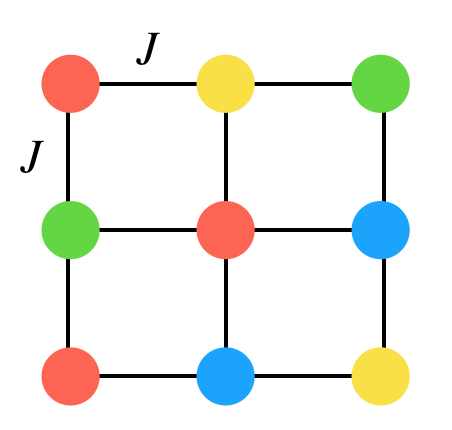
エネルギーの関数(ハミルトニアン)を以下で与えます。<i,j>は一番近いお隣で組み合わせをとるという意味です。

この式の意味としては、お隣のぷよと同じ色ならJ分のエネルギーを得ます、それ以外ならばエネルギー0です、という意味です。
例えば図中の赤は3連結になっているため3/2Jのエネルギーを得ています。(ダブルカウントがあるため2で割ります)緑も1/2Jを得ていますね。他のぷよは同じ色の連結が無いため0です。よってこの系のエネルギーは2Jと計算できます。
ここで注目して欲しいのは、このJというパラメータの符号です。この符号によってモデルの状態は大きく変わってしまいます。
まずJ<0の場合を考えてみましょう、この時はエネルギーの表式からお隣同士で同じ色になった方がいいことがわかります。(エネルギーは小さい方がお得です)
よってT=0のエネルギーだけで支配された世界では以下のような状態が実現します。*7

一方、J>0では全く逆の状況で、お隣と違う状態になろうとします。

つまり、この状態のように互い違いに色が配置されていると最低エネルギーとなります。
また、以下のように色々な色が入っていても同様です。
T=0においてJ<0では全て連結した状態、J>0では連結が全く無い状態という両極端なモデルを設定した時、温度によって平均連鎖数がどう変わっていくかみてみよう、というのが今回の目標となります。今後物理の用語に則ってJ<0のような相互作用を「強磁性相互作用」、J>0を「反強磁性相互作用」と呼びます。
強磁性モデル(q=4)
では早速みていきましょう。モデルのセットアップとしては、J<0(連結が増える方)で、取ることの出来る状態の数(ぷよの色の数)を4つに設定しました。今回は温度の効果も知りたいため、温度点を50個ほど取って高温から低温まで性質を調べています。
また、今回の計算は全てMCMCで回しています。(Lは前回と同様の定義で、普通のフィールドからの倍率を表します。)

まずはそれぞれフィールドにおいて物理量が定義できるためみていきます。(どうしても載せておかないと手が震えるので許してください)
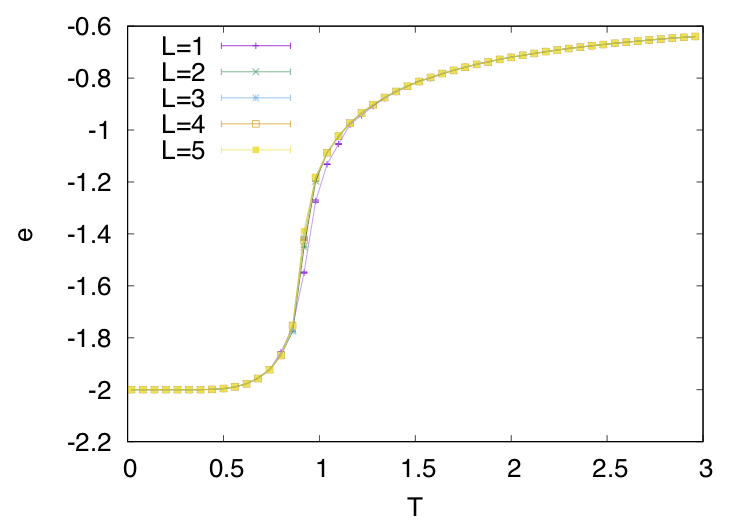
eはエネルギーで各温度に置ける1ぷよあたりのエネルギーをプロットしています。T=0に向かってどんどん小さくなっている様子がわかると思います。
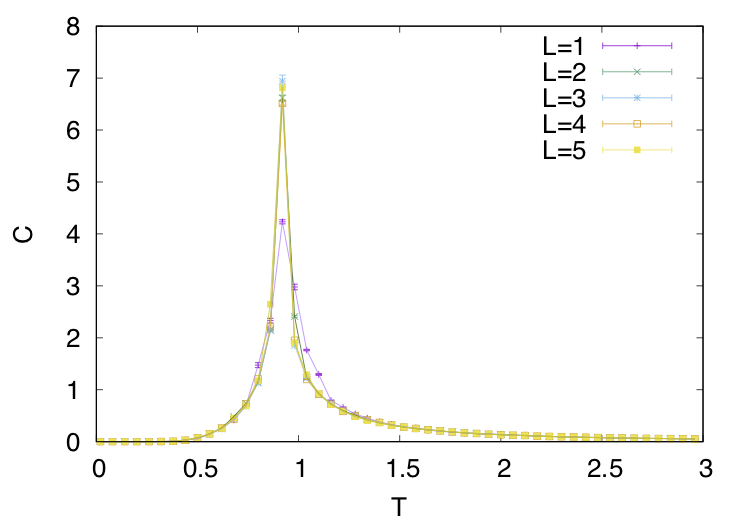
Cは比熱ですが、エントロピーの変化量(エントロピーの温度微分)を表します。大きなエントロピーを持っていた高温から低温に向けて徐々にエントロピーを下げていくのではなく、ある温度で一気にエントロピーを捨てていることがわかると思います。これが相転移温度です。*8
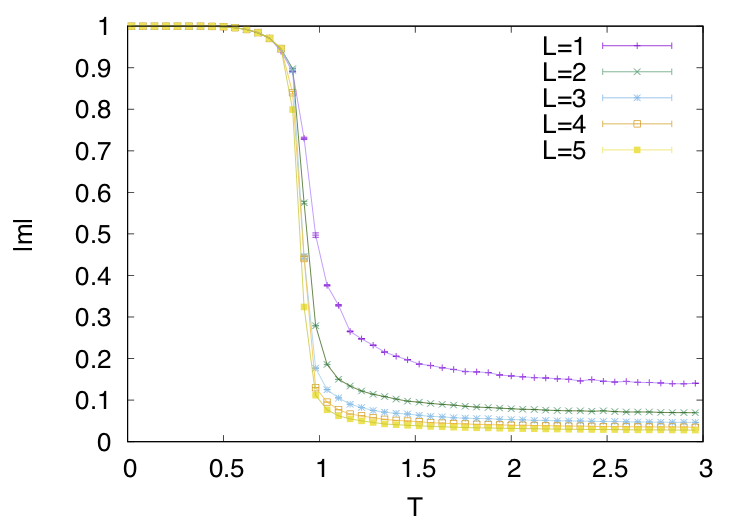
*9はそれぞれぷよがどれだけ揃っているか、逆にどれだけ揃っていないかの指標みたいなものだと思ってください。(ここでの揃っている揃っていないは連結の大きさです)
は全て連結していれば1していなければ0を取る物理量です。
はその逆です。T=0でm=1となってぷよが全て揃っていることが確認できると思います。高温ではどの色ぷよにもなれる離散的な対称性を持っていますが、低温ではそれが破られてある1色に制限されています。
それでは各温度点での連鎖数分布をみていきましょう。

値が集中しているところを拡大してみました。

やはり完全ランダムは超えていないように見えます。相転移に伴って平均連鎖数がどうなったのかみてみましょう。(T=3の点は便宜上表示していますがT=∞のデータです。)

今回の相転移温度を比熱からと見積もっていますが、その温度付近で平均連鎖数が最小になり、もっと温度を下げると全てが連結した状態になり、2連鎖へ収束する振る舞いが見えています。(全連結でも幽霊で2連鎖になります)
反強磁性モデル(q=3)
次は一転してT=0において連結が全く無い状態が実現している反強磁性的な系で考えてみましょう。
色ぷよの数qを3としているのは、このモデルがq>=4で相転移を起こさないためです。*10

同様に物理量をみていきましょう
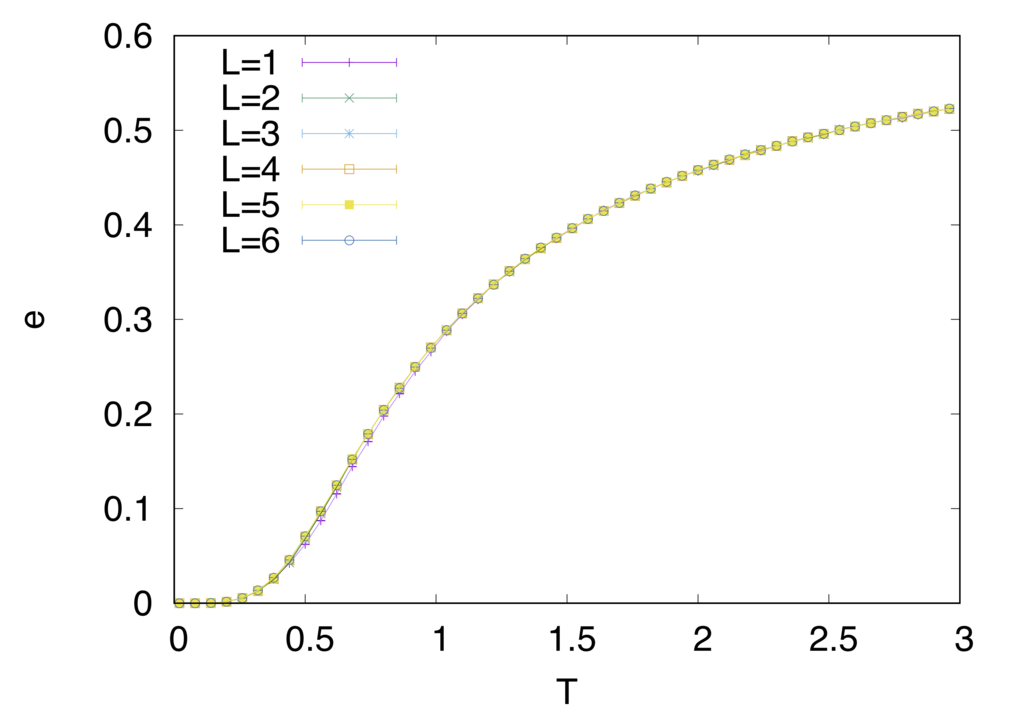
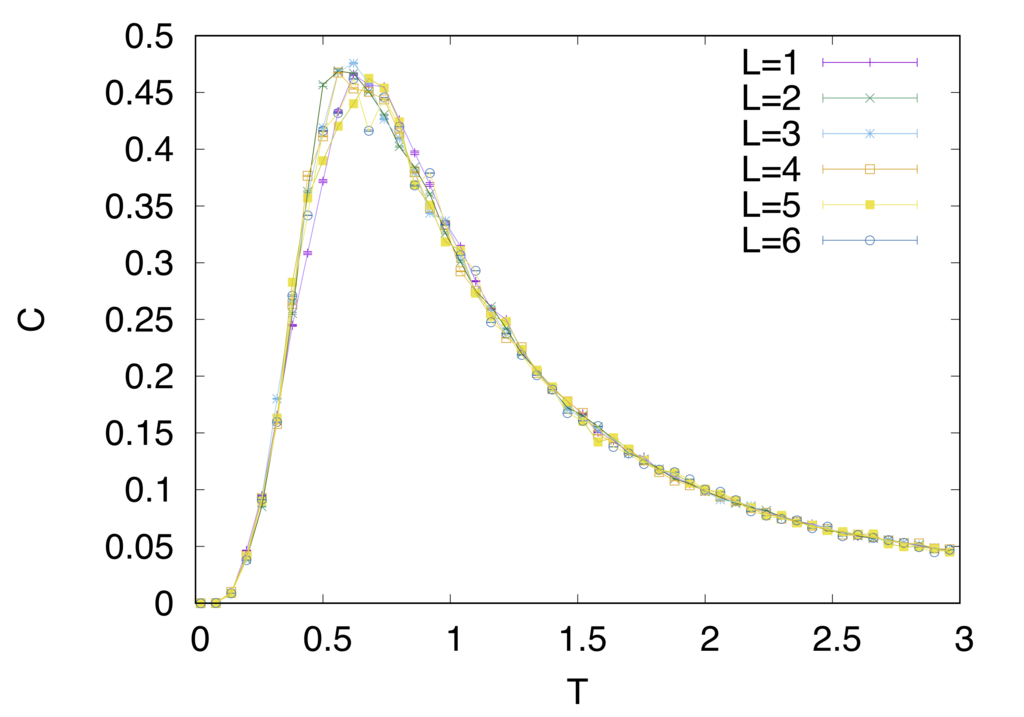
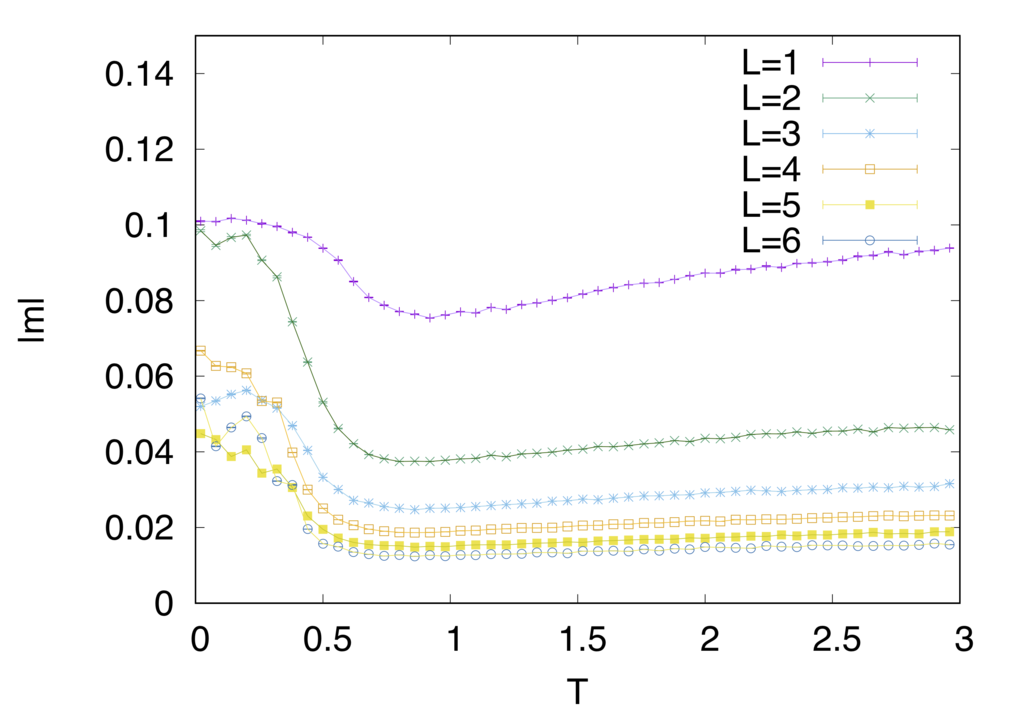
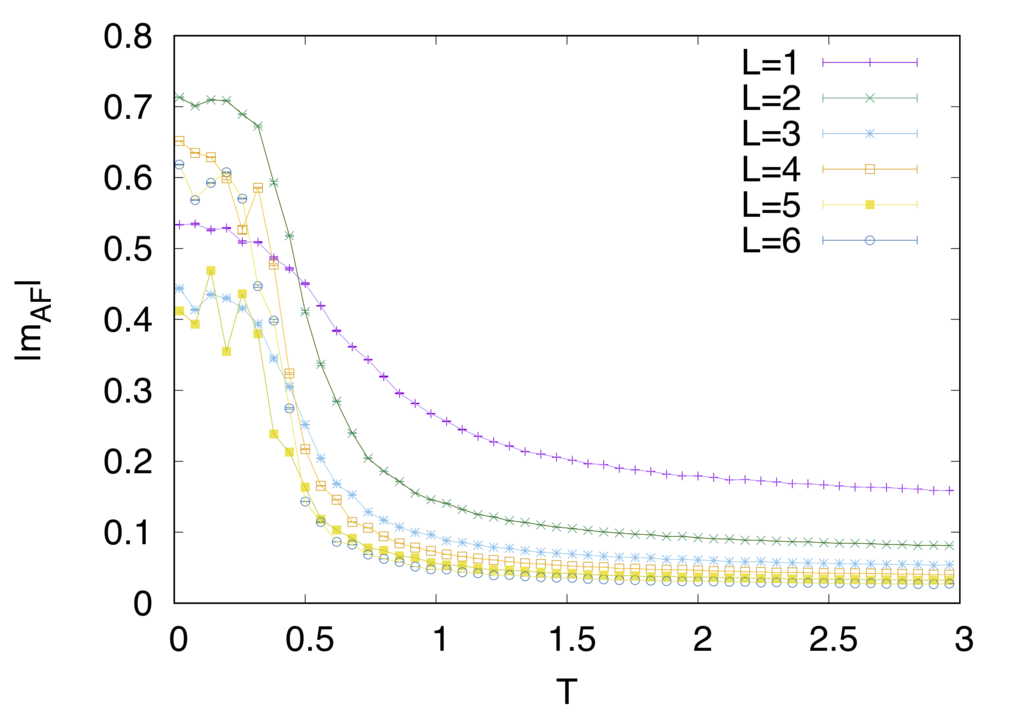
強磁性的なモデルとは一風変わった振る舞いをしているのがわかると思います。特に注目していただきたいのはエネルギーと比熱の振る舞いです。強磁性的な時には相転移温度でカスプ状になっていた比熱が鈍り、エネルギーの変化も穏やかなのがみて取れると思います。
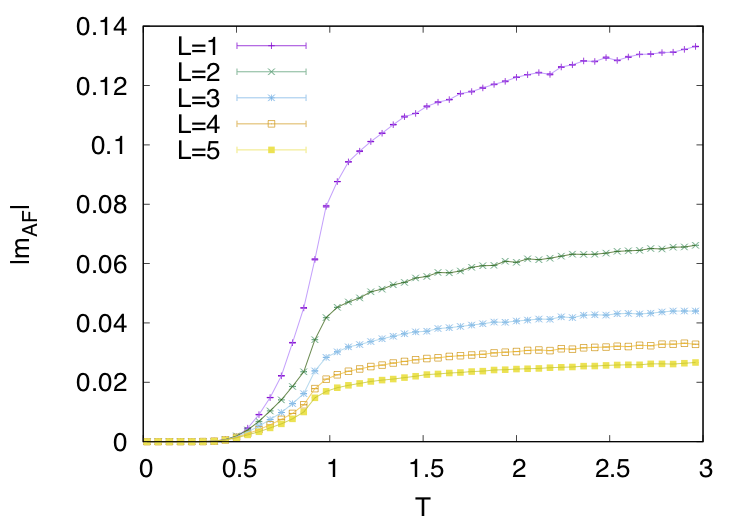
また、m,mAFの振る舞いもサイズに対して単純では無くなっています。(一応注釈10の論文値と整合性は取れていることを報告しておきます)
では平均連鎖分布をみてみましょう

これは期待が持てそう・・・!拡大してみます。

T=2あたりでランダムの平均連鎖数を越してそうですね、グラフにしてみます。

T=1.5-2付近で極値を持つことがわかると思います。ただし、この温度では相転移は起こしていないため"揺らぎ"の効果で連鎖が伸びているという結論になります。(結局は何が効いているかわからない・・・)
まとめ
今回はぷよぷよにポッツモデルを当てはめて、統計力学的(あるいは熱力学的)にフィールドを変化させた時の平均連鎖数の変化をみてみました。結果として、通常ぷよでよく用いられる4色ぷよでは完全ランダムにフィールドを埋めていった時の平均連鎖数を越えることができませんでした。フィールドが全部連結している状態からそれを一部変化させたものや、全く連結がない状態から変化させたものは連鎖にはあまりならないことから、もっと別の要素が必要そうということがわかりました。
色ぷよが3つの反強磁性モデルの場合は完全ランダムの平均連鎖数を越すことができましたが、秩序化する前の温度で増えていたため、今の所”揺らぎ”の効果でそうなったということ以上のことは言えなさそうです。
次の方向性ですが、全連結と0連結の中間の状態をもっと攻めることのできる相互作用や、"外場"を導入することを考えています。
全く別の方向としては、すでに完成された連鎖をポッツモデルに連想記憶として埋め込む方向も考えています。これは、前々回の記事と関わりがあり、ぷよの状態から相互作用を逆推定する問題を解くことになります。
沢山の完成した連鎖からの良さそうなJijを持ってくる、みたいな感じです。
めちゃくちゃ長くなりましたが、今回はこれで。
*1:あるエネルギーに対応する状態数の対数で定義される。具体的には,
:ボルツマン定数,
:あるエネルギーの値を取る状態の数
*2:十分に低温でもエントロピーが大きな値を取ることはあり得ます。例えばフラストレート系など巨視的な縮退がある場合は絶対零度でもエントロピーが0にならない場合もあります。
*3:より厳密には"ハミルトニアンの"対称性が破れている状況です。n成分ベクトルスピンはO(n)対称性を持ちますが、お互いが平行になるときエネルギーが最小になる状況ではSU(n)対称性が破れると考えます。これはエネルギーの保存を満たすためです。
*4:これを並進対称性といいます。
*5:氷の結晶は結晶構造としての並進対称性を持っていますが、水分子の並進対称性は破っています、このへんがややこしいですよね。
*6:だいたいq=6あたりから連続的な性質が見えてきます。具体的には最近接強磁性相互作用の元で、一昨年にノーベル物理学賞を受賞したKosterlitzとThoulessが提唱したKT転移というトポロジカル転移が見えるようになります。[J M Kosterlitz and D J Thouless Journal of Physics C: Solid State Physics, Volume 6, Number 7]
*7:より正確にはぷよの色の数だけ縮退しています
*8:自由エネルギーの一階微分量であるエネルギーに不連続な変化があるため、一次転移と呼ばれる転移で相が切り替わっています。
*9:の定義はPRL 45.1424(1980)より引用
*10:PRL 46.1458(1981)






