祭囃子は遠く、

祭囃子は遠く、

無職のハッピーエヴリディを書いていきます。

三日坊主

日記

あぶねえ・・・三日坊主になるところだった・・・。

日記

今日はジムに行ってきました。母親がジムジムうるさいので一緒に入会しました。
でもちょうど体力はつけたかったので、最高のタイミングです。

去年度は体力がなさ過ぎておぼれかけて死にそうになったり、帰りのバスに遅れかけて雪山に置き去りにされかけたりしました。
しかし、ジムに通うことで無限に泳げるようになり、スノーボードも上手になるでしょう。

おわりに

今週は珍しくほとんど予定が無い週で、早くもニートとしての素質が試されています。
今週は主にアルゴリズム体操してるんですが、統計の勉強もちょくちょく進めてます。
11月にある統計検定1級合格を目指してるんですが、どうなることやら。

今日のおすすめアーカイブ「アイドル部学力テスト」

これは・・・”番組”だ

www.youtube.com

■

日記
日記

今日は宮崎えびの市のぷよ大会にいってました。福岡から宮崎までブゥーーーーンしたんですが割と遠い。
田舎は交通費がめちゃかかるから結構金かかるんですよね。

大会自体は今回も楽しかったんですが、失得点差で敗退したので結構悔しかった・・・。
でも九州の大会はそこそこ勝てるから好きです。(関西では大体1回戦で負けるので)
あっ！レートでよく当たる人だ！みたいな人にも実際会えてわりと感動しました。

f:id:ta_ichi:20190406230336j:plain
中華料理”チャイナ”

おわりに

本日初顔出しぷよ実況をやらせてもらったんですが、難しいですね。
ぷよぷよが下手なのでよくわからないですし。

明日もウンカツ！(運転手活動)

運転手

日記
日記

今日は家のデスク周りの環境を整えようと思って、外に出かけていました。
実家には勉強机がもうないので普通のテーブルを改造する必要があります。
なにせ普通の机なので高さもなく、厚めの椅子に座ることすらできません。しかし、椅子に座らないとおしりがとても痛くなってしまうので買いに行くことを決意しました、車で。
買いそろえた結果が以下になります。

f:id:ta_ichi:20190405205635j:plain
tehu法でAtcoderのページを見せたいとかそういうわけではないです

おわりに

といいつつ競プロには触れますが、ぼちぼち再開することにしました。というのも弊社はわりとこういうのに力を入れてそうだからです。
あまりにしょぼいとマウントを取られかねないので、入社までに緑を抜けるくらいにはなりたいですね。

あとぷよらーkaggle部が発足したので早速なにかのコンペに出ようと思います。
今はこれに出ようと考えています。
www.kaggle.com
ざっと読んだ感じ株価予想かな？

明日はこれ行きます、楽しみ
puyo-camp.jp

無職

日記

お友達が日記をつけ始めたこともあって、僕もぼちぼち更新しようかなと思いました。

近状

4/1から晴れて無職になった僕なんですが、今のところ毎日がたのしいですね。
なんで無職なのかって話もありますが、そんなことはどうでもいいんです。今まで生きてきて基本的に学生でなかった時間はなかったんですが、こうして解放されてみると思ってたより不安がないというか、若い純粋な時間を使えるというドキドキ感の方が勝ってます。
ドキドキ感だけでは仕方ないもんで”上手く”使う必要があるわけなんですが、これがまだわからない。一応グダグダ一日を過ごす、ということはないんですが・・・。

日記

今日は朝起きてPCの環境を整えたり、過去のプログラムを整形したりしていました。案外人に見せることが大事、ということに気づいてきたので。
あと夜に寿司が食いたくなってきたので寿司を食べにいきました。くら寿司に行ったんですが、今回もまたびっくらポンをoffにしてしまいました、悲しい。

ところで、今度伊藤ライフ先生が策がしたVtuberがにじさんじからデビューしますね、チェックしていますか？僕は追ってるVtuberをリストで管理しているんですが、さっそく追加しておきました。

f:id:ta_ichi:20190404231048j:plain
実家で飼っている"強そうな猫"です。

おわり

あんまり長く書いたり面白くしようとすると一瞬でモチベなくなるんでこのくらいの無味さを保ってぼちぼち更新していきたいと思います。
最後におすすめのアーカイブでも貼っておきますね


エモくて百合と噂の「ライフ イズ ストレンジ / Life is Strange」を実況プレイ #1

卯月コウお得意の推察も面白いんですが、ゲームが良い。ただ最近長めのゲームをやる元気もなくなってしまいました、悲しいね。(だからこそ配信にはまっているのかもしれませんね)

ぷよぷよと連想記憶【準備編】

ぷよぷよ プログラミング

こんばんは、すしくんです。

今回は前回の
scitaku.hatenablog.com
この記事の最後の方で、pottsモデルにぷよのフィールドを連想記憶として埋め込みたいということを言っていたので、今回はそれをやってみました。

連想記憶については前々回の
scitaku.hatenablog.com
これを読むとなんとなくわかると思います。

目次

はじめに

前回言っていた通り、イジングモデルの逆推定問題(連想記憶)を拡張し、pottsモデルのパラメータをデータから逆推定するプログラムを書きました。
学習方程式は、イジングの場合とほとんど変わらなかったので、以下では結果を天下り的に書きます。
また、今回はデータを大量に準備する気力が湧かなかったので予備実験までの結果を載せて終わります。(誰かデータ作ってくれ)
一応学習方程式導出の詳細をアップしておきます。
・計算ノート
プログラムもgitにあげたいと一瞬思ったんですが、あまりに汚いのでやめました()

モデルと学習方程式

まずpottsモデルとはイジングモデルのように０か１だけでなく、０、１、２、…qー１の状態を取れるように拡張したモデルです。
難しく考えなくても、ぷよぷよのように赤ぷよ、青ぷよ、黄ぷよ…と状態を変化させられると考えると良いです。

f:id:ta_ichi:20181123010309p:plain

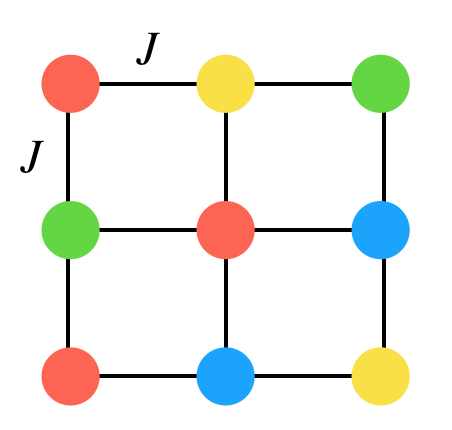
このモデルは上のように、様々な「色ぷよ」状態をとりつつ他の「ぷよ」と相互作用するようなモデルです。
実際のぷよぷよもある点に様々な色のぷよが存在していることからも、このモデルがぷよぷよをよく表現してくれそうという期待が持てます。
また、このモデルでは色ぷよの配置によってエネルギーを定義でき、今回は以下のように設定しました。\delta(v_i-v_j)はあるぷよviとvjが同じ色ならば１、違うならば０となるように定義しています。

U=\sum_{(i,j)}J_{ij}\delta(v_i-v_j)+\sum_{i}^{N}\sum_{\mu}^{q-1}b_i^{\mu}\delta(v_i-\mu)

J_{ij}は相互作用の強さで、負符号だと相互作用しているぷよと同じ色ぷよになりたがり、正だと違う色になりたがります。b_i^{\mu}はバイアス項(物理ではゼーマン項と呼ばれます)で、負符号の場合はあるぷよについてある値\muに対応した色ぷよにさせようとします。逆に正だと違う色にさせようとする効果があります。


以上を踏まえた上で、このモデルでぷよぷよのフィールドを再現する、というのは例えば階段連鎖を考えてみます。(一部切り抜いたフィールドと思ってください)
J>0として、簡単のため線で繋がれたぷよ同士に相互作用が働くことにしています。そうすると階段連鎖は、マイナス符号がついている組には同じ色ぷよがきて、正符号の相互作用が働くところには違う色が来て欲しくて…となっていることがわかると思います。(J,-Jは一部しか書いていませんが他のところも同様に考えられます)

f:id:ta_ichi:20181210214701p:plain

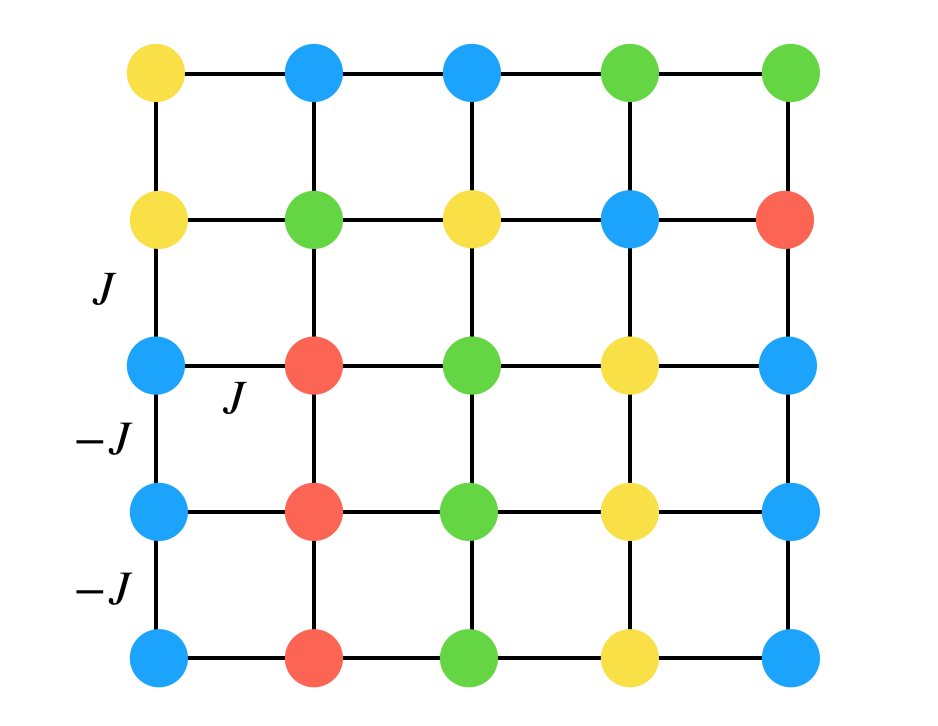
更に遠くのぷよと相互作用する組を考えると、例えばタブーの形にはならないようにパラメータを調整していけることがわかると思います。

このことからわかるように、pottsモデルにおいて「あるフィールドのデータから相互作用の強さと符号を推定し、連鎖において何が大事なのかを推定することが可能ではないか」と思って今回の遊びをはじめました。

また、詳しい人は疑問に思ったかもしれませんが、一般的なボルツマンマシンでは表からは見えない「隠れ変数」というものを導入します。これはeffectiveに３、４、５…体の相互作用を取り入れることができ、非常に強力です。しかし、今回はまずシンプルなモデルから出発したいのと、結果の解釈が難しくなることから採用していません。しかし、多体の効果は連結に対して効率よく損得を考えることができそうなので、いずれやってみたいですね。

さて、本題に戻ります。

pottsモデルの隠れ変数なしの一般的な学習方程式を天下り的に与えると

<\delta(v_i-\mu)>_{model} = <\delta(v_i-\mu)>_{data}
<\delta(v_i-v_j)>_{model} = <\delta(v_i-v_j)>_{data}

このようになります、上の式については\mu=0,1,..q-1についてそれぞれ別々に考えます。<\delta(v_i-v_j)>_{model}はモデルから\delta(v_i-v_j)という(物理)量を計算し、その平均値で近似することができます。<\delta(v_i-v_j)>_{data}は簡単で、入力したい(学習したい)データ全てに渡り平均をとればすぐに計算ができます。
要するにこの学習方程式は、データのある色がどのくらいあるかの平均(を１ぷよあたりに直したもの)と、モデルから計算される平均値を同じになるようにしなさい、ということです。二つ目は、データとモデルの間のあらゆるぷよ2つの組みの色関係を揃えなさいと言っています。
イメージとしては色ぷよの数だけイジングボルツマンマシンを並べて、それを二つ目の式で繋いでいるといった感じでしょうか？個人的には\delta(...)が結局イジングになるだけなので本質的には何も変わらないと思っています。(そっちの方が既存の手法が適用できて楽)

しかし、ぷよぷよの計算に以上の方程式を適用する場合、若干の不便さがあります。それは連鎖において「色そのもの」というのはなんの意味もないからです。
実際のフィールドを考えてみると

f:id:ta_ichi:20181211190039p:plainf:id:ta_ichi:20181211190037p:plain
この左右のフィールドでは何も本質的に違いはないです。左ではGTRの部分が青ですが右は赤、L字は…となっていますが色の位置関係さえ同じならば等価です。つまり、例えば「赤、緑、青、黄」に「１、２、３、４」と番号をつけて連鎖を記述した時、数字はそのままで色を1つ押し出すイメージで入れ替えて「黄、赤、緑、青」とみなした時の連鎖、「青、黄、赤、緑」、「緑、青、黄、赤」とした時は全て同じになります。
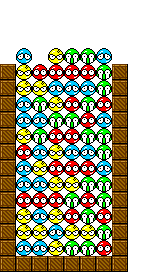
最初の色の並びを"回した"配列は変換の前後でフィールドを等価にします。
この対称性を考慮した上で今回の学習方程式は

<\delta(v_i-0)>_{model} = <\delta(v_i-0)>_{data}
<\delta(v_i-1)+\delta(v_i-2)+\delta(v_i-3)+\delta(v_i-4)>_{model} = <\delta(v_i-1)+\delta(v_i-2)+\delta(v_i-3)+\delta(v_i-4)>_{data}
<\delta(v_i-v_j)>_{model} = <\delta(v_i-v_j)>_{data}

今回は何もない空間にも状態を与えているため、０を対応させています。この学習方程式では、ぷよがない空間以外はバイアスが同じ値になり、色ぷよの変換に対する対称性を反映させることができます。

計算

では、具体的に学習方程式から学習がどのように進むかみていきましょう。
コードをあげない代わりにプログラムの流れだけ書いておきます。

  1. 学習データから<\delta(v_i-v_j)>_{data},<\delta(v_i-\mu)>_{data}を計算する
  2. フィールドに適当にぷよを配置する(ぷよが置かれない場合も今回は考慮しています)
  3. 温度アニーリングを用いながらMCMCの一種であるメトロポリス・ヘイスティングス法でフィールドを低温まで冷やす(その時のパラメータにおけるエネルギーが最小のぷよ配置を求める)
  4. \delta(v_i-v_j)などの(物理)量をサンプリングし、平均値を期待値と近似する。
  5. パラメータを勾配法を用いて更新する。(\etaは学習率)
    • _{new}b_i^{0} = _{old}b_i^{0} + \eta(<\delta(v_i-0)>_{model}-<\delta(v_i-0)>_{data})
    • _{new}b_i^{\neq0} = _{old}b_i^{\neq0} + \eta(<\delta(v_i-1)+\delta(v_i-2)+\delta(v_i-3)+\delta(v_i-4)>_{model}-<\delta(v_i-1)+\delta(v_i-2)+\delta(v_i-3)+\delta(v_i-4)>_{data})
    • _{new}J_{ij} = _{old}J_{ij} + \eta(<\delta(v_i-v_j)>_{model}-<\delta(v_i-v_j)>_{data})
  6. 更新した後3に戻り訓練回数分繰り返す

今回準備編であるため参考程度ですが、予備実験に用いたハイパーパラメータは(学習率、緩和に用いたMCステップ数、MCサンプリングの回数、最高温度、最低温度、温度点の数、訓練回数)
\eta=0.01,N_{mcmc}=100,N_{mcsmpl}=500,T_{max}=1.05,T_{min}=0.05,N_T=10,N_{train}=2000
このようにしました、パラメータの初期値は正規分布で適当に決めています。
温度についてですが、特徴的な温度スケールはせいぜい１オーダーなのと、Jijがランダムに入り混じった系は転移温度が低いため、多分１で十分高温だと思います。

さて、予備実験の結果をみてみましょう。今回はフィールドを２枚だけ記憶させました。(ちなみに左は僕が適当に作ったもので、右はももけんさんのGTRです)

f:id:ta_ichi:20181211190037p:plainf:id:ta_ichi:20181211195416p:plain

学習回数とパラメータの変化をみてみましょう、本当は全部確認すべき(というかlossとか尤度とかD_KLとか計算したいけどあまりわかってない)なんですが、適当に2つだけ抜き出してます。

f:id:ta_ichi:20181211203236p:plainf:id:ta_ichi:20181211203239p:plain

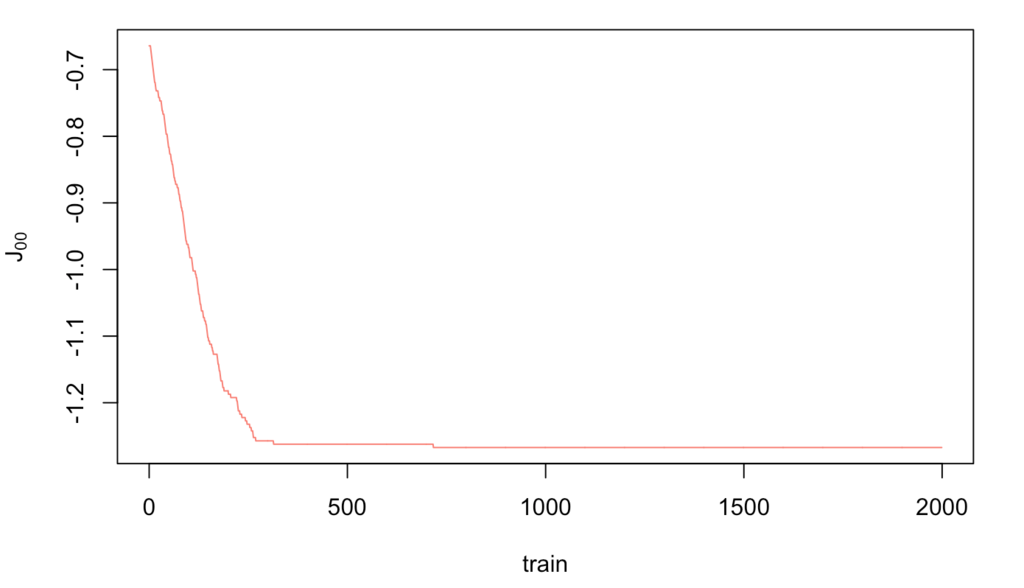
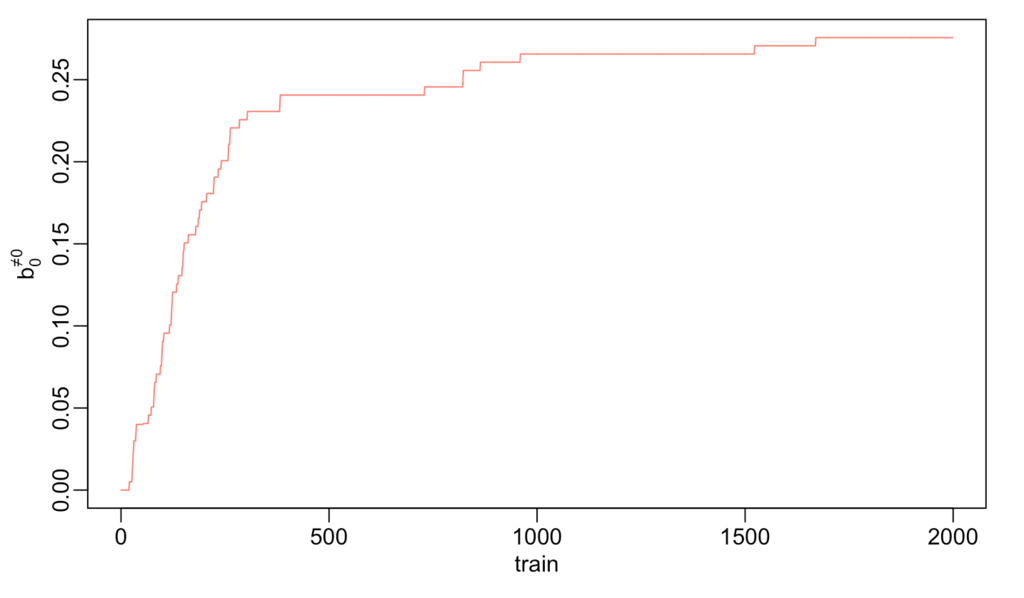
まぁある程度は収束してるから大丈夫かな・・・。

こうして学習が終了した後のパラメータで、MCMCで更新していくと2つの形のうちのどちらかが想起されます。
例えば左のような初期条件から学習済みパラメータで、低温まで冷やしていくと(エネルギーが最小のぷよの配置を求める)最終的には右のような、学習したGTRのうちの一つが出現します。

f:id:ta_ichi:20181211203753p:plainf:id:ta_ichi:20181211203755p:plain

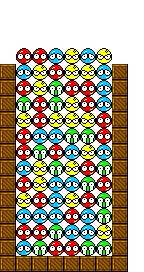
これだけみててもよくわからないので、パラメータについて見ていきましょう。

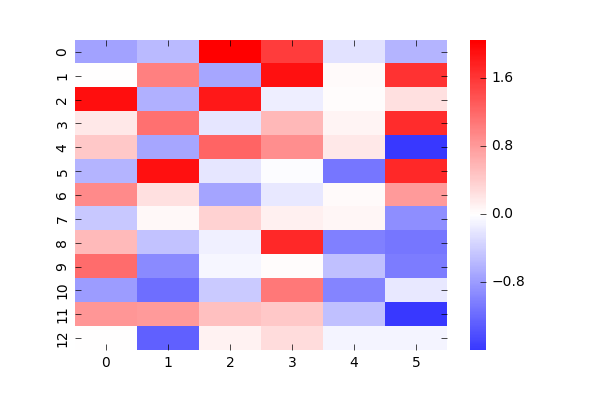
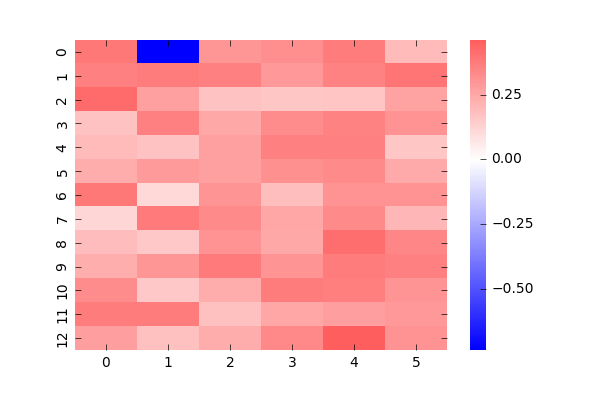
これは、あるぷよに対して他のぷよがどういう値で相互作用しているかの図です。赤は正符号での相互作用(違う色になりたがる)、青は負符号で(同じ色になりたがる)の相互作用で、濃さはその強さを表します。１つのぷよと他のぷよの関係を表しているため、全部載せると78枚になってしまうので適当に2つ持ってきました。(自分自身のところは０としています)
左図は(1,1)のぷよに対する相関でGTRの一番底です。期待としてはGTRの形が青で浮かび上がってくると思ったんですが、そうはなってませんね。おそらくデータが圧倒的に少ないため、他のパラメータで調整しているのだと思います。
右図は(2,11)のデータで、1つ目の学習データでぷよがなかったところです。ここも他に対して全て違う状態になる傾向が少し見えると思いましたが、見えませんでした。

f:id:ta_ichi:20181212010618p:plainf:id:ta_ichi:20181212010634p:plain

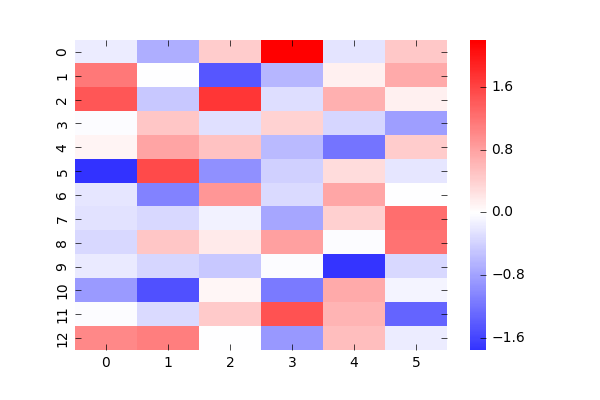
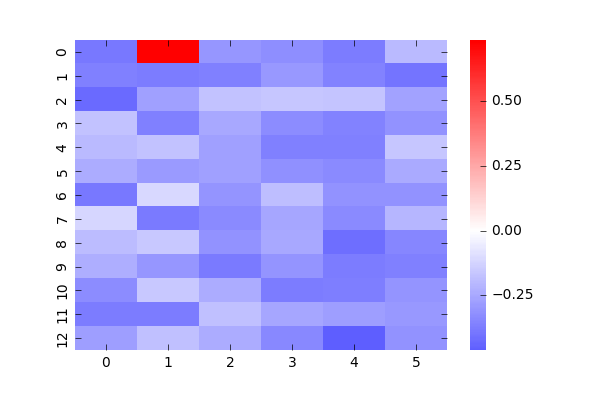
次にバイアスを見て見ましょう、これは_{new}b_i^{\neq0}と_{new}b_i^{0}で分けています。１枚目の学習結果を強く反映しているのがわかります。

f:id:ta_ichi:20181212011414p:plainf:id:ta_ichi:20181212011429p:plain

今回の軽い計算結果はここまでとします。

次回

今回はデータを集める気力がなかったので、まずは小さなデータで最低限期待されることが実現しているかなどをチェックする形になりました。期待通りのものもそうでなかったものもありますが、どのみちデータが足りないに尽きていると思われます。
次回は大量にデータを用意して学習した結果を報告できたらなぁと思います。
上手くいったら、いいなあ。

ぷよぷよと統計力学

ぷよぷよ プログラミング

こんばんは、すしです。

なんだか仰々しいタイトルですが、中身は大したことないです。今回は前回(以下リンク)の続きを書いていこうと思います。
scitaku.hatenablog.com

一応前回の記事を読まなくてもわかるように纏めますが、気になる方は読んでみてください。

目次

はじめに

前回はフィールドにぷよぷよをランダムに敷き詰めていったときに、発生する連鎖数の平均値を様々な大きさのフィールドで調べていきました。
結果的には僕たちがプレーしているフィールドを1として、アスペクト比を保ったままの倍率をLとするとその平均連鎖数はL^{0.6}程度になることがわかりました。
他にもお邪魔ぷよをフィールドに一定の割合でドープしてみたりしましたが、結局は完全ランダムに配置した時が一番連鎖の平均値が高いという結果でした。

そこで今回は「ぷよの生成過程にあるルールをつけて、ランダム生成の平均連鎖数を超えることができるのか？」というテーマでやっていきたいと思います。
僕たちが普段組んでる連鎖とは一体なんなのか、という問いに何か回答を与えることができたらいいなーくらいの気持ちでやってます。

統計力学の話

最初にあるルールでと書きましたが、今回は僕の専門である「統計力学」の範疇で与えられるルールでぷよをフィールドに生成していきたいと思います。

そこでまずは今回用いる統計力学の知識を簡単にですが纏めていきます。

イジングスピンとベクトルスピン

イジングスピンといえば割と聞いたことがあるという人も多いのではないでしょうか？
機械学習や量子コンピュータの分野で出てきたりするアレです。
元々は電子や陽子が持つ内部自由度で角運動量の次元を持つ物理量ですが、もっと簡単に言うと磁石の最小単位です。


f:id:ta_ichi:20181121002359p:plain

上の図のように、一番基本的なS=1/2ではスピンは上か下のいずれかを向いており、それがマクロに同じ方向に向いていると磁石になります。(上右図)
このように上か下かを向いている矢印を格子状に置いたモデルをイジングスピンモデルと言います。０か１の２状態を取ることからもなんかコンピュータぽくてそれっぽい応用ができそうな感じがしますよね。
量子コンピュータでは、古典的な描像である「上か下」でなく量子的な「上と下の状態の重ね合わせ」が重要になってきますが、今回は全て古典のお話です。

さて、離散的な状態を取るイジングスピンに対して連続的な状態をとるスピンがいても良さそうですよね？それがベクトルスピンモデルと言うもので、XY模型やHeisenberg模型などがそれにあたります。前者は２次元のベクトル(矢印)を扱い、後者は３次元のベクトルを扱います。量子スピンとのつながりでいくとS→∞の極限に対応していて(厳密にはS→∞,h→0,Sh=constの極限)、物質的にはS=5/2あたりから古典描像に近くなると言われています。(うろ覚え)
しかし、今回はあんまり出てこないので忘れていただいて結構です。

ハミルトニアンと自由エネルギー

ここから具体的な話になってきますが、今回のメインであるぷよ生成のルールについて話していきます。

統計力学では(それだけに限りませんが)モデルを動かすルールのことを「ハミルトニアン」と言います。
物理的にはエネルギーを与える関数(量子力学では演算子)ですが、ここではモデルにどういう風になって欲しいのか？を規定しているものだと思ってください。自然界において万物はマクロにはより安定な状態、つまりよりエネルギーが低い状態にいくため、エネルギーの関数を最小にする状態が実現します。統計に明るい人は損失関数だと思うと理解しやすいでしょう。

次に自由エネルギーについてです。ルールを決めているのはハミルトニアンと言いましたが、これは厳密ではありません。より厳密にはモデルの振る舞いはハミルトニアン(エネルギー)とエントロピー*1(乱雑さの指標)で決まります。具体的な表式は以下の通りで、これを最小化する状態が実際には実現します。

f:id:ta_ichi:20181121020224p:plain

T=0ではエネルギーが全ての振る舞いを支配していますが、T≠0ではエントロピーとの競合があるためエネルギーだけでは状態が決まらなくなります。
例えばスピンを2つだけ並べた状況を考えましょう。(ここではより一般的に長さ１のベクトルスピンを考えます)また、エネルギー関数Uは図中のものとします。

f:id:ta_ichi:20181121023558p:plain

まずT=0を考えるとFを最小化するスピンの配置はどうなるでしょう？この状況ではUのみを最小化すれば良いですね、つまり2つのスピンが平行になっている時U=-1となって最小値をとります。

f:id:ta_ichi:20181121232340p:plain

有限温度ではどうでしょうか？T<<1の時、エントロピーが十分に大きな値を取らない場合*2は、U=-1の状態が最小であるためスピンは基本的に平行でいようとします。基本的に、と言うところが重要で有限温度ではエントロピー項があるため、エネルギーで多少損してもこちらで得することが可能になります。要するに二つのスピンが平行な状態から揺らぐ(少しだけ違う方向を向く)ことが可能になるのです。今回のテーマではこの効果が重要な要素の一つになります。

f:id:ta_ichi:20181122011237p:plain

T>>1ではエネルギーを尊重するよりエントロピー項を尊重した方がお得になるため、なるべく乱雑になろうとします。その結果、エネルギーが最大になるスピンが反平行になる状態も実現します。これは身近な例でいくと、水は低温で綺麗な結晶構造を持ちますが(エントロピー低)、高温では気体になって好き勝手に動く(エントロピー高)ことに対応しています。

f:id:ta_ichi:20181121232719p:plain

前回の記事で若干触れましたが、ランダムフィリングの計算ではT→∞(またはU→0)の極限を考えていることに相当しているため、エントロピー(乱雑さ)だけで状態が決まっている状況と解釈することもできます。
ランダムフィリングは任意のハミルトニアンでの温度無限大での計算なので、今回は逆にT=0に近いところを考えていこうというわけです。

自発的対称性の破れ

ここまでの材料があってやっとこの話ができます。自発的対称性の破れと聞くと何年か前にノーベル賞を取られた南部先生のことを思い出す人が多いと思いますが、まさにその話です。(南部先生が受賞された研究領域は素粒子とかについてだったと思いますが、本質的には同じです。)

まず対称性とはなんでしょうか、例えばスピンは何も制限がなければ何処を向いてもいいですよね？

f:id:ta_ichi:20181122143649p:plain

これを連続対称性といいます。ベクトルの成分によりますが\vec{S}=(S_x,S_y)のようにかけるスピンなら平面、\vec{S}=(S_x,S_y,S_z)なら立体をぐるぐる回ることができます。

しかし、上の例のようにお互いの向きによってエネルギーが変わるような状況を考えると、Tが十分に小さい領域ではエネルギーを尊重します。よって、1つ1つのスピンは好き勝手な方向を向くことができなくなります。「いろんな方向を本来向くことができるにも関わらず、ある特定の方向を向いてしまう」ことを連続対称性*3の破れ、広くは自発的対称性の破れといいます。
温度が高いと無秩序な状態(対称性が高い)でいられますが、温度が十分に低いと秩序的(対称性が低い)な状態へ対称性が破れて変化します、これをもっと一般的な言葉では相転移といいます。

f:id:ta_ichi:20181122150417p:plain

また身近な例である水を取り上げます。例えばまず、気体状態の水は下図のように好きな方向へ動けますよね？*4この状態から温度を下げていくと皆さんご存知のように液体になり個体になります。これもある種の対称性を破って、相転移を起こして物質の状態が変わっている様子が見えていると言うわけです。*5

f:id:ta_ichi:20181122151612p:plain

ポッツモデルとクロックモデル

最後に今回のモデルとして採用したポッツモデル、そしてその仲間のクロックモデルの説明をします。

ポッツモデルとは一言でいえばイジングスピンモデルの拡張です。イジングモデルは上か下かの2つの状態をとるのに対して、こちらのモデルはq個の状態をとります。上でも下でもない状態、のように捉えるとなんだか難しい気になりますが、単純に赤ぷよ黄ぷよ青ぷよ…みたいな状態を考えると想像しやすいと思います。よって今回はこのモデルを用いてぷよぷよをモデル化しました。

次にクロックモデルはXY模型を離散化したものに対応しています。横着して図を使いまわしますが、下図のように\theta = \frac{2\pi}{q}の離散化されたq個の２次元ベクトルの内いずれかをとるモデルになっています。こちらはq→∞の連続極限が自然にXY模型に繋がるため、離散的な性質と連続的な性質を兼ね備えたモデルと言えます。*6

f:id:ta_ichi:20181122143649p:plain」

こちらのモデルで考える道もありだと思いますが、今回はポッツモデルを採用しました。

今回のお話

導入が長くなってしまいましたが、今回の具体的な内容について説明していきます。
モデルの説明をしてそれぞれの結果について述べていきたいと思います。

ぷよぷよとポッツモデル

導入でも話しましたが、今回はぷよぷよをポッツモデルに落とし込み、解析していきます。
エネルギーの関数(ハミルトニアン)を以下で与えます。＜i,j＞は一番近いお隣で組み合わせをとるという意味です。

U = J\sum_{\langle i,j \rangle}^{} \delta (S_i - S_j)
J:相互作用の強さ,S_i:ぷよ

f:id:ta_ichi:20181123005013p:plain

この式の意味としては、お隣のぷよと同じ色ならJ分のエネルギーを得ます、それ以外ならばエネルギー0です、という意味です。
例えば図中の赤は３連結になっているため3/2Jのエネルギーを得ています。(ダブルカウントがあるため2で割ります)緑も1/2Jを得ていますね。他のぷよは同じ色の連結が無いため0です。よってこの系のエネルギーは2Jと計算できます。

ここで注目して欲しいのは、このJというパラメータの符号です。この符号によってモデルの状態は大きく変わってしまいます。
まずJ<0の場合を考えてみましょう、この時はエネルギーの表式からお隣同士で同じ色になった方がいいことがわかります。(エネルギーは小さい方がお得です)
よってT=0のエネルギーだけで支配された世界では以下のような状態が実現します。*7

f:id:ta_ichi:20181123010114p:plain

一方、J>0では全く逆の状況で、お隣と違う状態になろうとします。

f:id:ta_ichi:20181123010239p:plain

つまり、この状態のように互い違いに色が配置されていると最低エネルギーとなります。
また、以下のように色々な色が入っていても同様です。

f:id:ta_ichi:20181123010309p:plain

T=0においてJ<0では全て連結した状態、J>0では連結が全く無い状態という両極端なモデルを設定した時、温度によって平均連鎖数がどう変わっていくかみてみよう、というのが今回の目標となります。今後物理の用語に則ってJ<0のような相互作用を「強磁性相互作用」、J>0を「反強磁性相互作用」と呼びます。

強磁性モデル(q=4)

では早速みていきましょう。モデルのセットアップとしては、J<0(連結が増える方)で、取ることの出来る状態の数(ぷよの色の数)を4つに設定しました。今回は温度の効果も知りたいため、温度点を５０個ほど取って高温から低温まで性質を調べています。
また、今回の計算は全てMCMCで回しています。(Lは前回と同様の定義で、普通のフィールドからの倍率を表します。)

f:id:ta_ichi:20181123142719p:plain

まずはそれぞれフィールドにおいて物理量が定義できるためみていきます。(どうしても載せておかないと手が震えるので許してください)

f:id:ta_ichi:20181123013254p:plainf:id:ta_ichi:20181123012947p:plain
f:id:ta_ichi:20181123013303p:plainf:id:ta_ichi:20181123013347p:plain

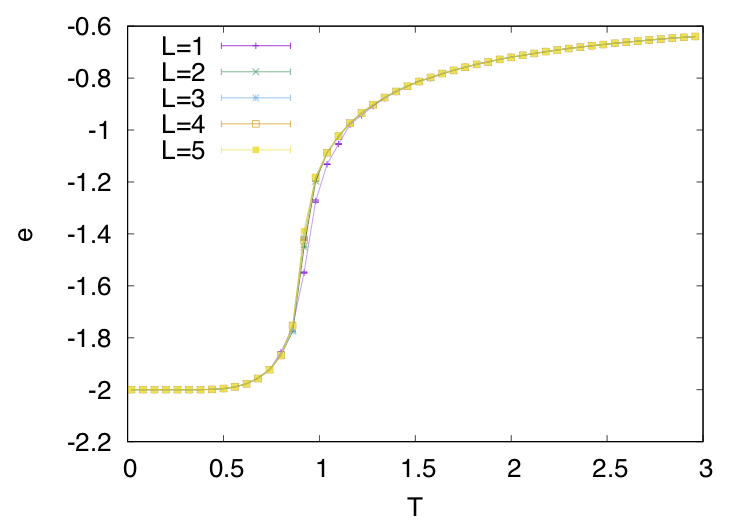
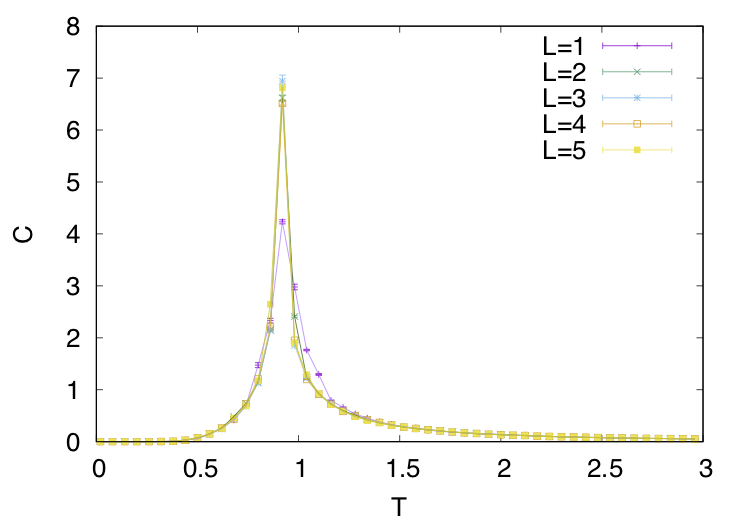
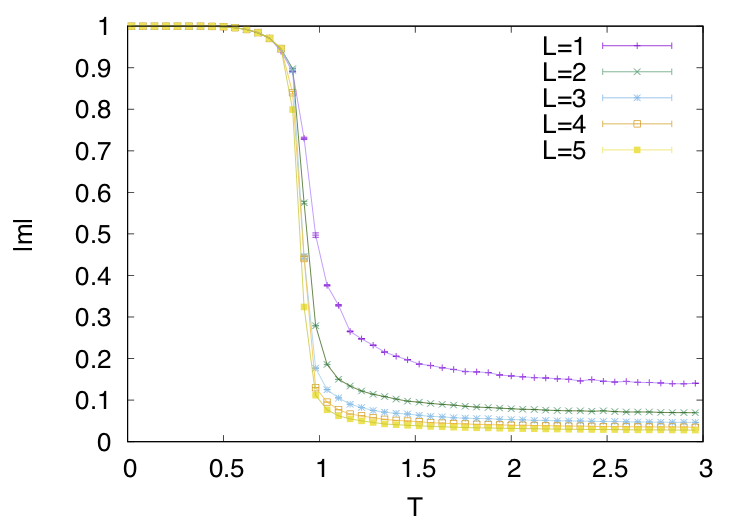
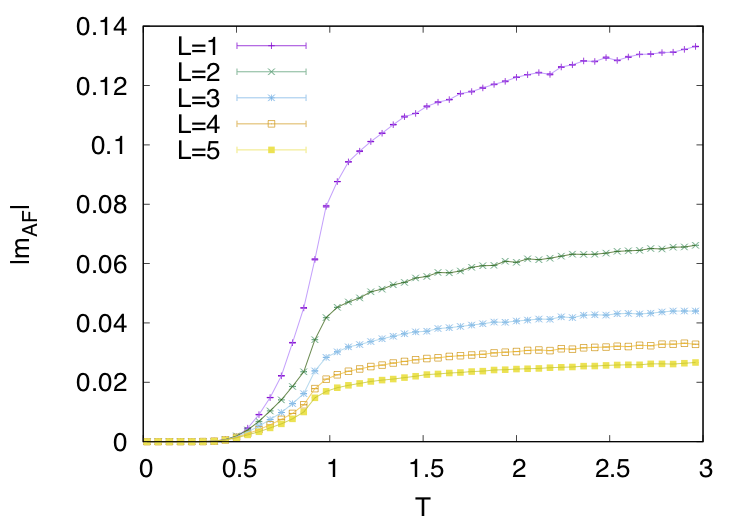
eはエネルギーで各温度に置ける１ぷよあたりのエネルギーをプロットしています。T=0に向かってどんどん小さくなっている様子がわかると思います。
Cは比熱ですが、エントロピーの変化量(エントロピーの温度微分)を表します。大きなエントロピーを持っていた高温から低温に向けて徐々にエントロピーを下げていくのではなく、ある温度で一気にエントロピーを捨てていることがわかると思います。これが相転移温度です。*8
m,m_{AF}*9はそれぞれぷよがどれだけ揃っているか、逆にどれだけ揃っていないかの指標みたいなものだと思ってください。(ここでの揃っている揃っていないは連結の大きさです)mは全て連結していれば1していなければ0を取る物理量です。m_{AF}はその逆です。T=0でm=1となってぷよが全て揃っていることが確認できると思います。高温ではどの色ぷよにもなれる離散的な対称性を持っていますが、低温ではそれが破られてある１色に制限されています。

それでは各温度点での連鎖数分布をみていきましょう。

f:id:ta_ichi:20181123172340p:plain

値が集中しているところを拡大してみました。

f:id:ta_ichi:20181123172452p:plain

やはり完全ランダムは超えていないように見えます。相転移に伴って平均連鎖数がどうなったのかみてみましょう。(T=3の点は便宜上表示していますがT=∞のデータです。)

f:id:ta_ichi:20181123172019p:plain

今回の相転移温度を比熱からT_c=0.92と見積もっていますが、その温度付近で平均連鎖数が最小になり、もっと温度を下げると全てが連結した状態になり、２連鎖へ収束する振る舞いが見えています。(全連結でも幽霊で２連鎖になります)

結論としては強磁性的な相互作用をもつぷよぷよのフィールドは相転移に伴って平均連鎖数が減るということになりました。

反強磁性モデル(q=3)

次は一転してT=0において連結が全く無い状態が実現している反強磁性的な系で考えてみましょう。
色ぷよの数qを3としているのは、このモデルがq>=4で相転移を起こさないためです。*10


f:id:ta_ichi:20181123174514p:plain

同様に物理量をみていきましょう

f:id:ta_ichi:20181123221411p:plainf:id:ta_ichi:20181123222704p:plain
f:id:ta_ichi:20181123221417p:plainf:id:ta_ichi:20181123221421p:plain

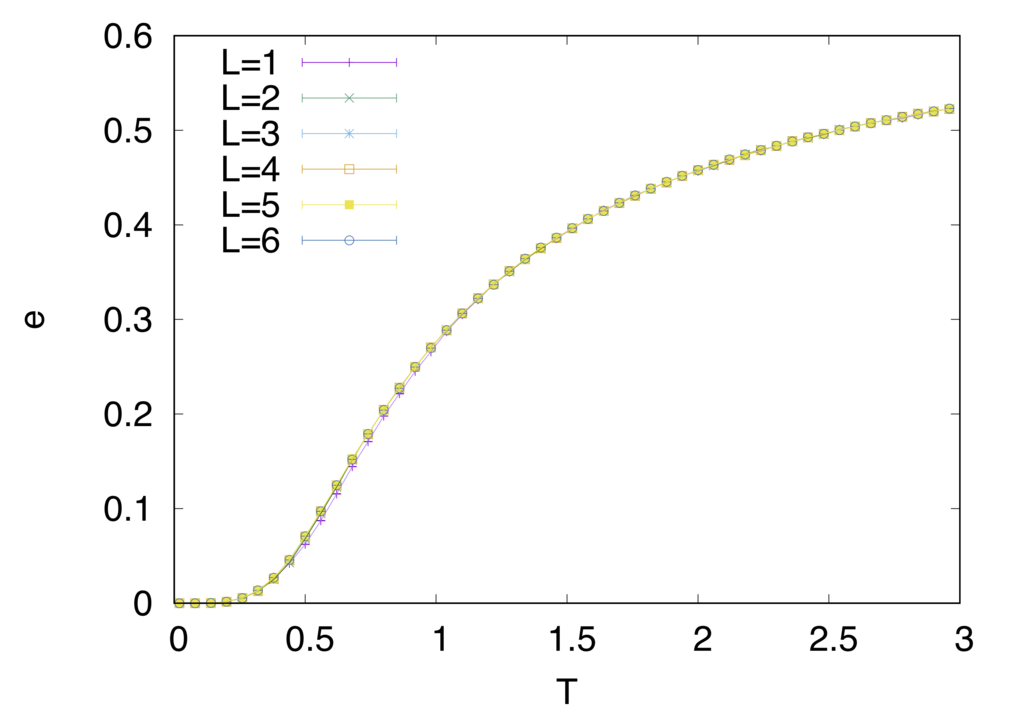
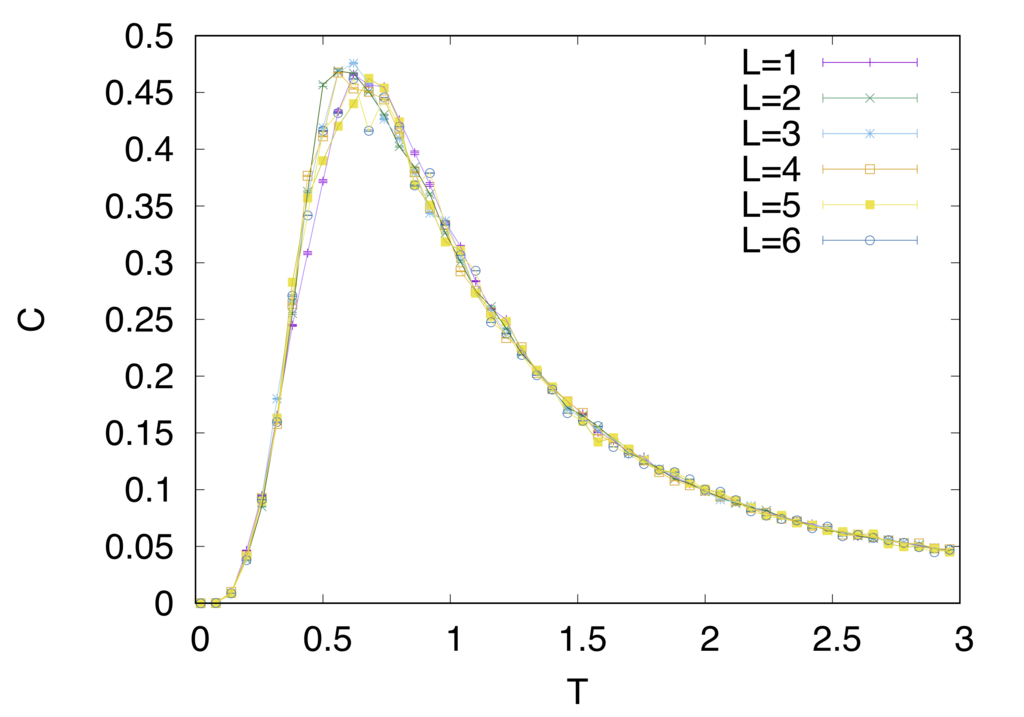
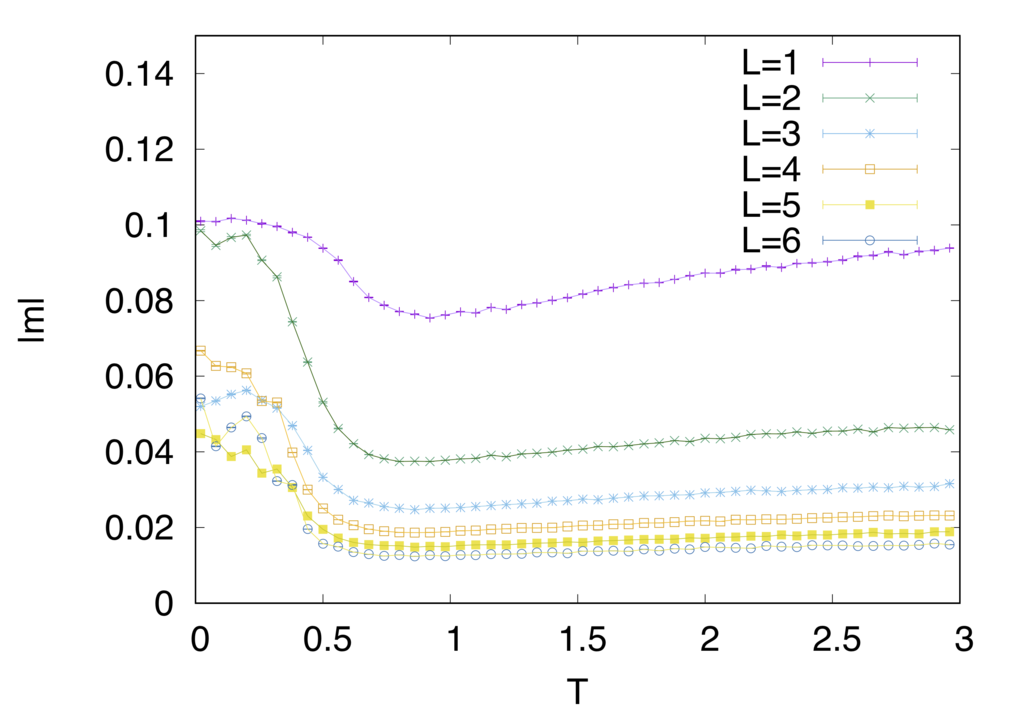
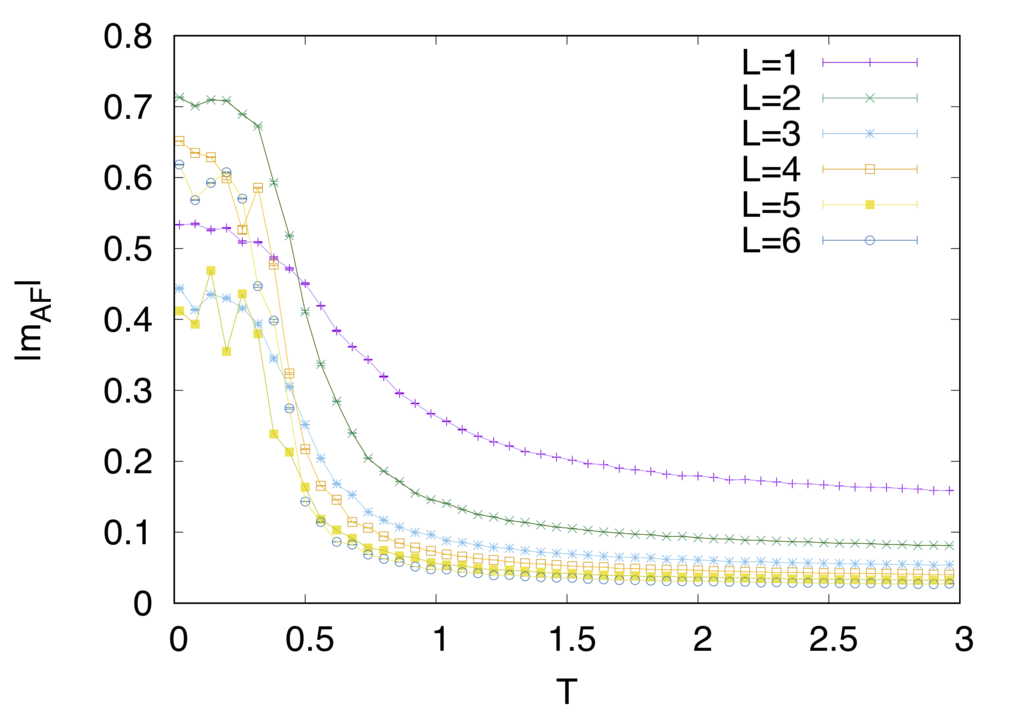
強磁性的なモデルとは一風変わった振る舞いをしているのがわかると思います。特に注目していただきたいのはエネルギーと比熱の振る舞いです。強磁性的な時には相転移温度でカスプ状になっていた比熱が鈍り、エネルギーの変化も穏やかなのがみて取れると思います。
また、m,mAFの振る舞いもサイズに対して単純では無くなっています。(一応注釈10の論文値と整合性は取れていることを報告しておきます)

では平均連鎖分布をみてみましょう

f:id:ta_ichi:20181124001649p:plain

これは期待が持てそう・・・！拡大してみます。

f:id:ta_ichi:20181124001849p:plain

T=2あたりでランダムの平均連鎖数を越してそうですね、グラフにしてみます。

f:id:ta_ichi:20181124002033p:plain

T=1.5-2付近で極値を持つことがわかると思います。ただし、この温度では相転移は起こしていないため"揺らぎ"の効果で連鎖が伸びているという結論になります。(結局は何が効いているかわからない・・・)

反強磁性モデル(q=4)

次は色ぷよの数を4つにしたものを考えましょう。このモデルは相転移を起こさないため、個人的には何も面白くないですが一応見てみます・・・。

まず物理量

f:id:ta_ichi:20181124002634p:plainf:id:ta_ichi:20181124002641p:plain
f:id:ta_ichi:20181124002642p:plainf:id:ta_ichi:20181124002645p:plain

特に何もいうことはありませんが、m,mAFに注目してみるとサイズをあげるごとにどんどん０に向かっていることがわかると思います。
これは有限温度ではぷよがデタラメな色になるからです。(連結が全くない、という秩序すら持ちません)

よって、相転移由来の連鎖への影響というものは何も見えませんが、一応同様にみていきます。

f:id:ta_ichi:20181124003101p:plain

すでにダメそうですが、拡大してみましょう

f:id:ta_ichi:20181124003138p:plain

各温度での平均連鎖数は

f:id:ta_ichi:20181124003208p:plain

単調に減少するのみですね・・・。

まとめ

今回はぷよぷよにポッツモデルを当てはめて、統計力学的(あるいは熱力学的)にフィールドを変化させた時の平均連鎖数の変化をみてみました。結果として、通常ぷよでよく用いられる４色ぷよでは完全ランダムにフィールドを埋めていった時の平均連鎖数を越えることができませんでした。フィールドが全部連結している状態からそれを一部変化させたものや、全く連結がない状態から変化させたものは連鎖にはあまりならないことから、もっと別の要素が必要そうということがわかりました。
色ぷよが3つの反強磁性モデルの場合は完全ランダムの平均連鎖数を越すことができましたが、秩序化する前の温度で増えていたため、今の所”揺らぎ”の効果でそうなったということ以上のことは言えなさそうです。

次の方向性ですが、全連結と0連結の中間の状態をもっと攻めることのできる相互作用や、"外場"を導入することを考えています。

全く別の方向としては、すでに完成された連鎖をポッツモデルに連想記憶として埋め込む方向も考えています。これは、前々回の記事と関わりがあり、ぷよの状態から相互作用を逆推定する問題を解くことになります。
沢山の完成した連鎖からU = \sum_{\langle i,j \rangle}^{}J_{ij} \delta (S_i - S_j)の良さそうなJijを持ってくる、みたいな感じです。

めちゃくちゃ長くなりましたが、今回はこれで。

*1:あるエネルギーに対応する状態数の対数で定義される。具体的にはk_bln(W),k_b:ボルツマン定数,W:あるエネルギーの値を取る状態の数

*2:十分に低温でもエントロピーが大きな値を取ることはあり得ます。例えばフラストレート系など巨視的な縮退がある場合は絶対零度でもエントロピーが０にならない場合もあります。

*3:より厳密には"ハミルトニアンの"対称性が破れている状況です。n成分ベクトルスピンはO(n)対称性を持ちますが、お互いが平行になるときエネルギーが最小になる状況ではSU(n)対称性が破れると考えます。これはエネルギーの保存を満たすためです。

*4:これを並進対称性といいます。

*5:氷の結晶は結晶構造としての並進対称性を持っていますが、水分子の並進対称性は破っています、このへんがややこしいですよね。

*6:だいたいq=6あたりから連続的な性質が見えてきます。具体的には最近接強磁性相互作用の元で、一昨年にノーベル物理学賞を受賞したKosterlitzとThoulessが提唱したKT転移というトポロジカル転移が見えるようになります。[J M Kosterlitz and D J Thouless Journal of Physics C: Solid State Physics, Volume 6, Number 7]

*7:より正確にはぷよの色の数だけ縮退しています

*8:自由エネルギーの一階微分量であるエネルギーに不連続な変化があるため、一次転移と呼ばれる転移で相が切り替わっています。

*9:m_{AF}の定義はPRL 45.1424（1980）より引用

*10:PRL 46.1458（1981）

ぷよぷよとランダムフィリング

ぷよぷよ プログラミング

こんにちは、すしくんです。

突然ですがみなさんこのツイート知っていますか？

統計物理専攻としてはなかなか興味を惹かれるものがあって、これをこうしたらどうなるんだろう・・・とか色々気になったものです。
しかし、当時はプログラミングが今よりも下手くそだったので、自分で解析することが叶いませんでした。最近は少しマシになったので自分でプログラムを組めたのでこの記事に至ります。


目次

はじめに

タイトルにもある通り今回は先行研究に従い、まずはランダムフィリングで色々条件を変えていったときに連鎖の分布がどう変化するかを見ていきます。具体的にはアスペクト比を保ったままスケールを変えていったときの平均連鎖数や、お邪魔ぷよを一定の割合で入れたときの変化です。
ランダムフィリングとは文字の通りですが、フィールドにぷよをランダムに敷き詰めていくことです。したがって一番の違いは現実のぷよぷよでは不可能な状況も発生するところです。(例えばフィールド真ん中から連鎖が始まる、１２段３列目にぷよがあっても良いなど)
今回はとこぷよや対戦面を含めた盤面への主張はしないので、この場合こうなるんだとかそのくらいに思ってください。


プログラムの流れ

  1. あるスケールでのフィールドに４色のぷよをランダムに配置
  2. 連結を判定し、４連結以上でぷよを消す
  3. 連鎖数を測定
  4. 最初に戻る

拡張されたフィールドにおける連鎖数分布

まずは一応最初にやられている結果をフォローできるか確認しましょう。
また、記号についてですが１３行６列のフィールドをL＝１としています。２６行１２列はL＝２、３９行１８列はL＝３…と最初のフィールドからの倍率を表すものになっています。

L＝１(先行研究)の結果です

f:id:ta_ichi:20180815142208p:plain

ピークの２−３連鎖がほぼ等しく、あとはlinearぽく落ちるとことかも似てるように見えますね。まぁこれでよしとしましょう

次にフィールドを等倍していったときの分布を見てみましょう。

f:id:ta_ichi:20180815142823p:plain

重なってて見えにくいですが、どのサイズもピーク左側が急峻で右側が緩やかな分布になっています。
分布の形自体はこの範囲内で収束しているように見えるため、どのサイズでも左右非対称で有限の歪度がある分布であることは間違いなさそうですね。

分布の形についてはわかったので次は量的なところをみていきます。
この比較だとLをどんどん大きくしていくと分布がどんどん右に動いていくだけで面白くありません。そこで各サイズでの最大連鎖数でスケールされた連鎖数で比較していきましょう。

f:id:ta_ichi:20180815143647j:plain

ピークに注目すると大きなサイズほど０に近づいていっているように見えますね。ここからわかることは、フィールドの最大連鎖数の増え具合よりも、ランダムフィリングしていったときの平均連鎖数の増え具合の方が緩やかということです。
最大連鎖数は\frac{13*6*L^2}{4}と計算していますが、せいぜいL^2のオーダーでしか増えません。一方平均連鎖数はこれを下回っていることが予測されます。

確認のためスケールされた連鎖数の期待値をみてみましょう

f:id:ta_ichi:20180815144838p:plain

緩やかにL→∞に向かって０に収束していきそうな感じが見えてますね。

片対数で見てみましょう(これでlinearならば指数関数的)

f:id:ta_ichi:20180815145006p:plain

うーん、綺麗な下凸でしょうか
両対数はどうでしょう(これでlinearならばべき関数的)

f:id:ta_ichi:20180815145134p:plain

これも微妙ですね、L＝３以上でわりかし線形にも見えますが大まかには上凸でしょうか？

L＝３以上でフィッティングかけてみましょう

f:id:ta_ichi:20180815145534p:plain

小さいサイズはものも見事に外れますね・・・
しかし大事なのはこのべき関数がどうなっているかです。

f:id:ta_ichi:20180815145821p:plain

ax^bという形でフィッティングしているので、−1.4程度で落ちていることがわかりました。
あんまり確かめるまでもなかった気はしますが、スケールサイズLに対して平均連鎖数はL^{0.6}程度のべき関数で抑えられそうということは一応やらないとわからなかったですね。
ただ、統計警察は気づいていると思いますが、これはフィッティング(回帰)させるモデルが多分ダメです。上の画像真ん中あたりのReduced chisquareに注目するとめちゃくちゃ小さいことがわかります、この値はだいたい１程度のオーダーだとよくフィッティングできてるなあという気持ちになるんですがこれは少し疑ったほうがいいですね。(多分)

ーおまけー
上の図から考えると、Lを大きくしていったときに早く収束するモードと遅く収束するモードがあると考えるのが自然でしょう。そこで補正項を入れてax^b+cx^dという形でフィッティング
f:id:ta_ichi:20180815150541p:plainf:id:ta_ichi:20180815150547p:plain

一応合わせるだけなら可能ですが、本当に合わせただけですね。もっと真面目にモデルを考えないと多分ダメです。

一定の割合でお邪魔ぷよを含むフィールドにおける連鎖数分布

今度はフィールドを固定してお邪魔ぷよをある一定の割合pで混ぜたときの分布をみてみましょう。
期待としては、ほどほどのお邪魔ぷよは多連結を切って連鎖になる方向に向かわせるはずなので、割合に対して平均連鎖数は上凸になる、と思ってました。(ました)

f:id:ta_ichi:20180815161207p:plain

0.05とか0.2とかがお邪魔ぷよの割合です、ダメそうですね、期待はずれです、普通に連鎖が減るだけです。

割合と平均連鎖数の図もみてみましょう。
f:id:ta_ichi:20180815161406p:plain

対数でみてみましょう
片対数
f:id:ta_ichi:20180815161423p:plain
両対数
f:id:ta_ichi:20180815161430p:plain

単調に減少していってますね・・・。

一応フィッティング、よくわからないので２次関数で合わせます。(どうせ適当な冪函数だし)

f:id:ta_ichi:20180815161903p:plain
f:id:ta_ichi:20180815161912p:plain

まぁ微妙ですねw


ただ、そもそもこのヒストグラムの出し方はもしかしたらよくないかもしれません。
おそらくもっとちゃんとやるならば、レプリカ法の精神に乗っ取って

  • ある割合でお邪魔を配置する
  • その隙間をぷよで埋める
  • 連鎖数を測定
  • ２、３を何度も繰り返してヒストグラムを取る
  • 同じ割合でまたお邪魔配置、2へ
  • こうしてできた「あるお邪魔配置でのヒストグラム」のアンサンブル平均をとる

とやるのが良さそうです。(めんどいからやらない)
今の解析でも割と大きなサンプルサイズではあると思うのでそこまで結果は変わらない気がします。

まとめと次の話

簡単にまとめると

  • ランダムフィリングにおいて最大連鎖数がL^2で増えるのに対し平均連鎖数はそれよりも緩やかにしか増えない
  • お邪魔ぷよは単純に平均連鎖数を下げる

といったところですね。

さて、次の進め方ですがアスペクト比を変えるとか、フィールドの倍率変更＋お邪魔とかあると思いますが面白くなさそうなのでもっと違うことをします。
というか本来こっちがやりたかったことなのですが(専門なので)

「あるハミルトニアン(コスト関数)にしたがって統計力学的にフィールドを作る」

ということをやりたいと思います。(統計的にはq-state potts modelと等価)
どういうことかというと、例えばあるハミルトニアン(エネルギーと思ってください)を考えます。

\mathcal{H}=J\sum_{(i,j)_{NN}}^{}\delta_{p_i,p_j}

\delta_{p_i,p_j}はクロネッガーのデルタ、p_i,p_jは最隣接のぷよぷよです。このとき、Jが負だとするとこのエネルギーを最小化する解は「全てのぷよが同じ色」となることはすぐにわかると思います。正だと逆に連結が一切ないフィールドが解です。(piなどには色に対応する数字が入ってると考えてください)

このようにフィールドの状態はある程度この関数でコントロールすることができます。期待的には、フィールド一面に連結している状態と一切連結していないフィールドの中間を見るとそこそこ連鎖してくれそう。
さらに「温度」の概念も導入することで、温度揺らぎからくる効果により「盤面一色がエネルギー最小であるが何個かのぷよは違う色になる」ことができます。
これも連鎖の助けになりそうです。

このことから「ハミルトニアンの式そのもの」と「温度」をうまく組み合すことができればランダムフィリングで得られた平均連鎖数を越すことができるかもしれません。
連鎖数が多い方がエネルギーが低いという式を指定すれば連鎖数は増えるのでは？という意見もあると思います、しかしそれは結果が自明であり面白くないのでやりません。(そうしてできた形を見るのは面白いかもしれません)

また、今回やったことは「任意のハミルトニアンにおけるT→∞の性質」を見たと言い換えることもできます。このあたりも次の記事の導入で話したいと思います。