ダンロン3プレー 〜1回目の自由行動
ダンロン3を始めたので今の時点での予想を抽象的にでも書いておく、既プレイはニヤニヤして腕組みでもしててください。
1,2と進めたところまでのネタバレはすこーしだけあるのでやってない人は見ないでください。
追記したりしてもしかしたら情報足すかも。
■全体的な謎
雑に予想していく、まだよくわからんので抽象的な予想。
- 鳥籠になっていて外が分からないが、外がどうなってるか分かっても脱出は厳しいねぇ〜ってなるタイプそう → 箱庭モノは大体そう
- モノクマのことを最初は知ってそうだったので時系列的には1,2の後ぽい
- モノクマーズのピンクの言いぶり的には複数回同じことが行われている感じもするので、ゲームを通して何かしらの目的がありそう? → 1みたいな動機ではなさそう
- 初回特典は卒業→外に出れるなのか不明瞭だった気がするからこの辺トリック絡んできそう
なんかよくわからんけど重要そうなことも適当に
- なくなった記憶そのものというより記憶の無くし方とかそのへんが重要そう
- モノクマーズが5体もいる理由
- 校内の外にはでれるのに内部から外に出られなさそうな封鎖がしてある理由、そもそも荒れ果てている理由
あとはグチ
- アクションダルそう
- マリオみたいなやつ操作性悪すぎ
- 捜査パートに脳のリソースを割きたくないので動かすみたいなやつ要らない(どの程度使うかわからんが)
■キャラの所感とか予想
赤松楓
- 可愛い
- 希望→未来ときて何になるか
- 才能的にも今までと根本的に違うタイプの立ち位置を見せつけてきそう(最後のワンマン感をなくすとかそもそもそういう展開にならないとか)
入間美兎
- 下品
- キャラ的には料理人と同じなので死にそうだが女ポイントで延命
- 発明ポジ(左右田ポジ)はしばらくは重宝しそうなので少なくとも中盤まではいそう
王馬小吉
- 見た目からすでにCV下野
- 若干のバックボーンの謎を抱えているので最初には死ななそう
- ヤクザと同じ感じで疑われつつも最終生き残りそう寄り
天海蘭太郎
- 流石にすぐ完全退場しなそう
- 消す前の記憶がありそう
- 終盤までいそう筆頭
キーボ
- 覚醒パートありそう
- 殺されそう、死んだとき殺人に当たるのかというくだりがありそう
獄原ゴン太
- 毎回いる筋肉枠
- 狼(だっけ)に育てられたこと自体が大きく関わってくる瞬間がありそう
- 飼育員ポジと被りきらないように動きそう
- 終盤手前くらいまでいそう
最原終一
- 女かハゲ、あと女なら多分レズ(確信)
- 本当の才能は探偵ではなさそう
- 流石に終盤あたりまでいそう
真宮寺是清
- 多分ブリーチにいた
- 中盤で殺されそう
茶柱転子
- 早めに死にそう
白銀つむぎ
- コスプレしたあと死にそう(役目を終えるので)
星竜馬
- 意外と死なないなってくらいのタイミングまでいそう
- 謎の事件を抱えてるので最初には死ななそう
東条斬美
- 多分レインが好き
- 序盤〜中盤で人殺しそう
春川魔姫
- 声と顔面が良い
- 思ったよりデカい謎を抱えていそう
- 死なないでほしいけど死にそう
百田解斗
- 多分バカ
- 生き残りそう
夢野秘密子
- 一回手品披露したら役目を終えそう
夜長アンジー
- 人殺しそう
一旦以上。
スクレイピングから機械学習するまでのDockerfile
pytorchの公式イメージをベースとしてスクレイピング系とboosting系を乗っける。
jupyter-labも使える。
想定としてはwebのデータをNN系とboosting系で機械学習する人向け。
自然言語系の環境も整えたいけどやったことないからだれか・・・
chrome-driverのバージョンは自分が使っている(であろう)ブラウザから「ヘルプ→chromeについて」みたいなところからバージョンを確認して揃える。
※2022年7/4時点では以下で動作確認。
Dockerfile
FROM pytorch/pytorch:latest
ENV TZ=Asia/Tokyo
RUN ln -snf /usr/share/zoneinfo/$TZ /etc/localtime && echo $TZ > /etc/timezone
RUN apt-get -y update \
&& apt-get -y upgrade \
&& apt-get install -y unzip zip tzdata git wget gnupg
RUN apt-get install -y libgl1-mesa-glx libglib2.0-0 libsm6 libxrender1 libxext6
# chrome
RUN wget -q -O - https://dl-ssl.google.com/linux/linux_signing_key.pub | apt-key add && \
echo 'deb [arch=amd64] http://dl.google.com/linux/chrome/deb/ stable main' | tee /etc/apt/sources.list.d/google-chrome.list && \
apt-get update && \
apt-get install -y google-chrome-stable
# chrome driver(ドライバのバージョンは適切なものを入れる)
ADD https://chromedriver.storage.googleapis.com/103.0.5060.24/chromedriver_linux64.zip /opt/chrome/
RUN cd /opt/chrome/ && \
unzip chromedriver_linux64.zip && \
rm -f chromedriver_linux64.zip
# labは最新のを入れる
RUN python -m pip install --upgrade pip
RUN pip install jupyterlab
RUN pip install ipywidgets
# seleniumも最新の入れる
RUN pip install selenium
RUN pip install bs4
RUN pip install oauth2client
# requirements.txtのインストール
WORKDIR /app
ADD requirements.txt /app
RUN pip install -r requirements.txtrequirements.txt
※僕の趣味で何個か無駄なライブラリが入ってる(tweepyとか)
lxml==4.9.1 matplotlib==3.5.2 pandas==1.4.3 scikit-learn==1.1.1 seaborn==0.11.2 sympy==1.10.1 opencv-python==4.6.0.66 opencv-contrib-python==4.6.0.66 tweepy==4.10.0 schedule==1.1.0 tensorboardX==2.5.1 torchsummary==1.5.1 xgboost==1.6.1 lightgbm==3.3.2 catboost==1.0.6
pytorchでKeras風の学習と出力をする
本題の通りpytorchでKeras風の学習と出力をするプログラムを作りました。
Keras風と言っているのは単純にmodel.fit(~)みたいな感じで学習して、verboseまわりが同じ感じになるってだけです。
そもそもpythonが下手なのでそんなに大層なことはできません。
指摘や文句は@scibeanまで
モチベーション
最近pytorchを使いはじめたんですが、ずっとKeras使ってたので学習周りで少し手間取ったのと、lossとかaccとか表示してくれないのが不満だったので。
正直pytorchの良さを殺してしまっている恐れもありますが・・・知らんけど。
前提
今回はdocstringを綺麗に書こうキャンペーンで丁寧目に作ったので基本そちらを見ればいいんですが一応前提は以下
くらいでしょうか。cpu対応とかmulti-gpu対応とか別に難しくはないんですが、めんどくさいのと後者に至ってはデバッグ環境がないので諦めました。
コード
こっちは最新化しないので、最新版はgitを見てください
github.com
class keras_model(): """ keras風のトレーニング+出力にするクラス GPU計算+1GPUが前提 Attributes ---------- model : net pytorchで作ったモデル epoch : int epoch数 dataloader : DataLoader 訓練データ criterion : torch.nn lossの種類 optimizer : optim pytorchのoptimizerクラス scheduler : scheduler putorchのschedulerクラス validation : DataLoader validationデータ accuracy : function accuracyを返す関数。デフォルトはクラス分類を想定(=出力がスカラ)。 引数と出力はdefault_accuracyと同じである必要がある step_num : int step数 """ def __init__(self,model=None): """ Parameters ---------- model : net pytorchのモデル """ self.model = model self.epoch = None self.criterion = None self.optimizer = None self.scheduler = None self.dataloader = None self.accuracy = None self.validation = None self.step_num = None if model is None: raise ValueError("model is None!") def train_step(self,images,labels,val=False): """ 1step分の学習をする Parameters ---------- images : Tensor (batch_size,C,H,W)のTensor labels : Tensor 正解ラベルのTensor val : bool ,default False Trueのとき評価モード Returns ------- pred : Tensor 推論された値のTensor loss : float lossの値 """ optimizer = self.optimizer model = self.model criterion = self.criterion scheduler = self.scheduler if val: images = images.cuda() labels = labels.cuda() out = model(images) loss = criterion(out, labels) return out.max(1)[1],loss.item() optimizer.zero_grad() images = images.cuda() labels = labels.cuda() out = model(images) loss = criterion(out, labels) loss.backward() optimizer.step() if scheduler is not None: scheduler.step() return out.max(1)[1],loss.item() def fit(self,epoch=None,dataloader=None,criterion=None,optimizer=None,scheduler=None,validation=None,accuracy=None): """ モデルの学習を実行 Parameters ---------- epoch : int epoch数 dataloader : DataLoader 訓練データ criterion : criterion lossの種類 optimizer : optimizer pytorchのoptimizerクラス scheduler : scheduler or None, default None putorchのschedulerクラス、指定は任意 validation : DataLoader or None, default None validationデータ、指定は任意 accuracy : function or None, default None accuracyを返す関数、指定は任意。デフォルトはクラス分類を想定(=出力がスカラ)。 引数と出力はdefault_accuracyと同じである必要がある """ self.epoch = epoch self.dataloader = dataloader self.criterion = criterion self.optimizer = optimizer self.scheduler = scheduler self.accuracy = accuracy self.validation = validation self.step_num = len(dataloader) if epoch is None: raise ValueError("epoch is not None") if dataloader is None: raise ValueError("dataloader is not None") if optimizer is None: raise ValueError("optimizer is not None") for e in range(epoch): print("Epoch {}/{}".format(e+1,epoch)) step_t=0 step_acc=0 step_loss=0 n_sample=0 model.train() for i,(batch_images,batch_labels) in enumerate(dataloader): start_step_t = time.time() preds,loss = self.train_step(batch_images,batch_labels) if accuracy is None: acc = self._default_accuracy(preds,batch_labels) else: acc = accuracy(preds,batch_labels) end_step_t = time.time() step_t+=end_step_t - start_step_t step_acc+=acc step_loss+=loss n_sample+=len(batch_labels) acc = step_acc/n_sample loss = step_loss/(i+1) self._keras_like_output(step=i,acc=acc,loss=loss,t=step_t) if validation is not None: v_loss=0 v_acc=0 n_sample=0 model.eval() with torch.no_grad(): for i,(batch_images,batch_labels) in enumerate(validation): val_preds,val_loss = self.train_step(batch_images,batch_labels,True) if accuracy is None: val_acc = self._default_accuracy(val_preds,batch_labels) else: val_acc = accuracy(val_preds,batch_labels) v_acc+=val_acc v_loss+=val_loss n_sample+=len(batch_labels) val_acc = v_acc/n_sample val_loss = v_loss/(i+1) self._keras_like_output(step=i,acc=acc,loss=loss,val_loss=val_loss,val_acc=val_acc,t=step_t,val=True) print("") def _default_accuracy(self,preds,labels): """ accuracyを計算 Parameters ---------- preds : Tensor 推論結果のTensor labels : Tensor 正解ラベルのTensor Returns ------- acc : float 精度 """ acc = (preds == labels.cuda()).sum() return acc.item() def _keras_like_output(self,step,acc,loss,t,val=False,val_loss=None,val_acc=None): """ kerasのverboseぽい出力 Parameters ---------- step : int 何step目か acc : float 各stepまでにおける精度の平均 loss : float 各stepまでにおけるlossの平均 val : bool or, default False validation結果の出力か否か val_loss : float or None, default None validationのlossの平均 val_acc : float or None, default None validationの精度 """ if val: l = self.step_num epoch = self.epoch step_p = (step+1)/l bar = "=" *30 result = " - loss:{:.4f} - acc:{:.4f} - val_loss:{:.4f} - val_acc:{:.4f}".format(loss,acc,val_loss,val_acc) print("\r {}/{}[{}]-{:.2f}s{}".format(l,l,bar,t,result), end="") else: l = self.step_num epoch = self.epoch step_p = (step+1)/l bar = "=" *int(step_p*30)+">" + " " *(30-int(step_p*30)+1) if step_p==1: bar = "=" *30 result = " - loss:{:.4f} - acc:{:.4f}".format(loss,acc) if val_acc is not None: result = " - loss:{:.4f} - acc:{:.4f} - val_loss:{:.4f} - val_acc:{:.4f}".format(loss,acc,val_loss,val_acc) print("\r {}/{}[{}]-{:.2f}s{}".format(step+1,l,bar,t,result), end="")
使い方
イメージとしてはtorchのモデルをkerasのモデルっぽい新しいクラスにしてfit関数を使うイメージ
import time #必須 #~必要なライブラリの読み込み~ #~任意のデータの読み込み(DataLoaderクラスである必要性がある)~ model = Net()#任意のモデル model.cuda() criterion = nn.CrossEntropyLoss().cuda()#モデルによって適切なものに変える optimizer = torch.optim.SGD(model.parameters(), lr=0.0005, momentum=0.99, nesterov=True)#モデルによって適切なものに変える scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer,lambda epoch: 0.95 ** epoch)#適切なものにする(schedulerはなくても良い) k_model = keras_model(model=model) k_model.fit(criterion=criterion,optimizer=optimizer,epoch=10,dataloader=trainloader,validation=val_loader,scheduler=scheduler)
※動作イメージ図

最後に
- gpuの指定もうちょっと柔軟にしたいかも
- lossとかaccのあるエポックの出力までに置けるstepでの平均というのがどの程度正当化されるかよくわかってない(かと言ってstepごとにしても・・・)(そもそもkerasはどう計算してる?)(そもそも平均とかの計算あってる?)
- kerasにある機能をもっとつけたいかも?(save_weightsとかはあっても良さそう)
- kerasにはないけど色々表示させたりもしたい、学習率とか
- 少しプログラムに無駄があるので改善したい
本気で読んだ論文まとめ
本気で読んだ論文を簡単にまとめていく記事にしたいと思います。あとなるべく前提知識を必要としない感じで書いて資料に詳しい説明を書きたい。
From complex to simple : hierarchical free-energy landscape renormalized in deep neural networks
DNNモデルを統計力学的に解析して、なぜデータ数に対して多いパラメータを決めることができるのかを調べた論文。
資料
輪講で使った資料を置いておきます。(後半はちょっと失速しているのであとで足したい・・・)
背景
- 現在の機械学習はモデルのパラメータ数に対してデータ数が少ないの学習できている(と信じられている)
設定
- DNNモデルを対象とし、教師データとモデルの出力が一致する重み空間を解析することで、学習済みモデルの比較をする。
- 解析計算では解析を可能にするためにデータ間に弱い相関を持たせている
- "gap"からeffectiveなコスト関数を出してシミュレーションの計算もしている
結果
- 入力、出力層の近くの重みパラメータはどの重みのサブセットを取ってきてもオーバーラップがそこそこある
- 対照的に中間層はオーバーラップがなく、特に決まった値を取る必要がない(中間層は適当に決めて良い?)
- シミュレーションは上の結果を支持する形で得られた。
課題
- データ間に弱い相関を入れたのがどこまで正当化されるか
- データ数とニューロンの数の比を保ったまま無限大に飛ばす操作がどこまで正当化されるか
ギモン
- gapについて、中間層でも符号を揃える必要はあるのか?
- teacher/student settingのRSB解のもじり方がわからない
ひとくちめも
目次
tensorflow-gpuを入れる(for Windows)
最新のやつ入れる。インストーラー起動してC++とpythonのとこにチェック入れるのを忘れずに
- 公式ホームページ(ソフトウェア要件から各種リンクあり)
www.tensorflow.org
ここからCUDA10.0と~for cuda10のcudnnの最新バージョンを入れる。ただインストーラー立ち上げて推奨設定でおk
公式を見るとtensorflow-gpuはcuda9しか対応してないように見えるけど、最新のやつ(2019/7/21 tf ver 1.14)はCUDA10がないと動かないみたい。
- ライブラリインストール
ここまで終われば
pip install tensorflow-gpu pip install keras
- GPU確認
from tensorflow.python.client import device_lib device_lib.list_local_devices()
- mnist(keras)でチェック
- cupy導入
pip install cupy-cudaバージョン
でインストール(pip install cupyだとダメだった)。今回は以下のようにする
pip install cupy-cuda100
Conda promptへのエイリアス設定
基本コマンドプロンプトと同じノリ
参考サイト
qiita.com
doskey ls=dir doskey /macros > %USERPROFILE%\macros_conda.txt
conda promptのショートカット→プロパティのリンク先の末尾に以下を追加
& doskey /macrofile=%USERPROFILE%\macros_conda.txt
dockerからjupyterを手軽に起動させる例(Windows)
doskey jp=docker run -v "%cd%":/home -w /home -p 8888:8888 --rm -it kaggle/python jupyter notebook --no-browser --ip="0.0.0.0" --allow-root
あと使いそうなのはactivateとか?$*は引数
doskey ac=activate $*
上記まとめ
doskey ls=dir doskey jp=docker run -v "%cd%":/home -w /home -p 8888:8888 --rm -it kaggle/python jupyter notebook --no-browser --ip="0.0.0.0" --allow-root doskey ac=activate $* doskey /macros > %USERPROFILE%\macros_conda.txt
kaggleやろおぜ(環境構築編)
こんばんわ、周りのオタクたちがkaggleの機運を高めているので環境構築について色々調べていたら気になるものが
ば・・・爆速!?環境構築が一瞬で終わってしまう夢のような話があるのか。
読んでいくとDockerを使ってやっているらしい。
Dockerとは

Docker(ドッカー[2])は、コンテナと呼ばれるOSレベルの仮想化(英語版)環境を提供するオープンソースソフトウェアである[3]。VMware製品などの完全仮想化を行うハイパーバイザ型製品と比べて、ディスク使用量は少なく、仮想環境 (インスタンス) 作成や起動は速く、性能劣化がほとんどないという利点を持つんですよね。
まぁ早い話が、アプリとかライブラリとかOSとかひとまとめにしたやつをガシャガシャ動かせるやつみたいなもんだと思ってます。
実際に触り始めて1日しかたってないんで間違ってたら許してね。
これを使えば機械学習とかに使うライブラリをひとまとめにしたやつがババンと作れるわけですからそりゃ早いよねって。
対象・前提
対象は僕のようなPC初心者の赤ちゃんから、この辺はよく知らない大人までです。
詳しいことは理解しなくてもnotebookを開けるように書いたつもりですが、細かいところで動作確認取ってないやつあるのでおかしかったら教えてください。
僕自身あまり詳しくないので、ふんわりとしかDockerの詳しい説明とかもろもろしません。
許してね。
上の記事とこれ読めば大体わかるから頑張りましょう。(ところどころコマンドミスってるけど)
qiita.com
導入方法
基本的には上の通りにやったら一瞬で終わります。
ただ、上のやつって自分の手元にあるPCにDocker Image(環境そのものが全部詰まってるやつ)を持ってくるわけなんで、めちゃくちゃ容量食うわけです。
kaggleの公式imageだと17Gbくらいかかります。
そこで、クラウドでやりましょう!という話になります。
今回おすすめするのはGCP(Google Cloud Platform)です。
console.cloud.google.com
AWSもよさそうですが、まじめに使ったことがないのでこちらで説明していきます。
GCPは初回特典として300ドル分のクーポンをくれるので結構アドです。
まずは左上あたりにあるところからプロジェクトを作りましょう(kaggle-ichimuraとなってるところ)

これ初回ログインの画面ではないから、もしかしたら初ログインしたら手順通りにやっていくと勝手に作らされるかも。
そして「三」みたいなボタン押してVMインスタンスを作成します。
その後作成を押すと実際にVMのスペックを設定するところが以下のように出てきます。
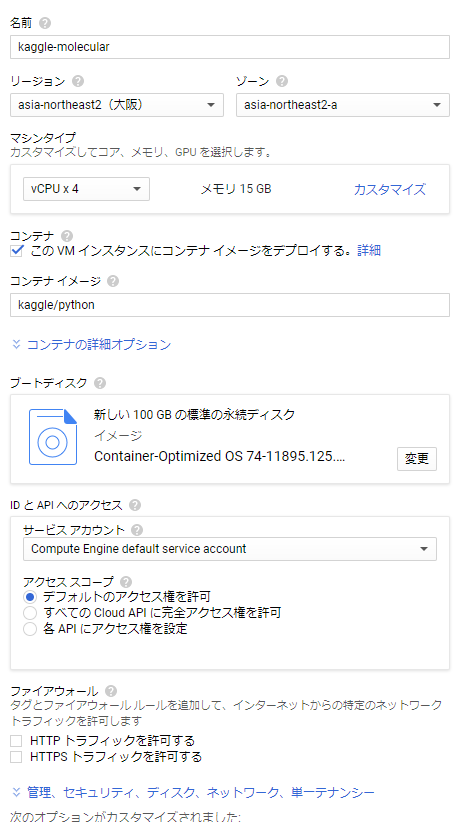
名前は適当に決めます。リージョンとゾーンは、近いやつを適当に選びました。この画面の右側に1時間当たりいくらとか出てくるので、そこと相談しながら決めましょう。
CPUやストレージについてもお好みで設定してください。僕は画面の通りに設定しました。
大事なのが「VMインスタンスにコンテナイメージをデプロイする」ってところで、ここにチェックを入れて「kaggle/python」と打ちましょう。
そうすると勝手にkaggle公式のDocker ImageをVMに導入してくれます。
ただ、立ち上げ直後は各種DLで表示されません。しばらく待ってください(5敗)
その間に以下を導入しましょう。
cloud.google.com
GCPの操作が色々楽になります、例えばSSH認証とか通信とかもう全部勝手にやってくれます。
導入したら専用のshellができるので(windows)それで
gcloud compute ssh --zone {インスタンスのゾーン} "{インスタンス名}"で通信ができるようになります。
入ったら、
docker images
で「kaggle/python」があるか確認してください。なかったらもう少し待つか、VMを作り直してみたりしましょう。
ここまで完了すればもう環境自体は目の前にあります。
確認出来たら
docker run -p 8888:8888 -v $PWD:/home --name test -it kaggle/python bash
でコンテナ(VM上にできる実際の環境)を作成します。
docker runは、基本的に「docker run -it {image名} そいつにやらせたいこと」みたいな形をしています。
上のコマンドは
-pでポートのなにがしか(このあたりわかんなすぎて辛い)
-vでVM上のディレクトリをコンテナ内の:以下から参照できるようにする(コンテナの中にデータを蓄えることは基本しない)。$PWDはVMのカレントディレクトリを勝手に代入してくれます。
--nameでコンテナの名前
-itで用いるimage
でbashを実行しますとなります。
例えば
echo "print(\"Hello World\")" > test.py docker run -v $PWD:/home -w /home --rm -it kaggle/python python test.py
とやるとなるほどにゃんこになれると思います。
--rm は実行ごとにコンテナを使い捨てるオプションで、-wはコンテナのカレントディレクトリになります。
-vでコンテナのhomeディレクトリとVMのカレントディレクトリを引っ付けてるので、そのままtest.pyで実行できているわけです。
そんなこんなでコンテナの中に入れたら
jupyter notebook --ip=0.0.0.0 --allow-root
と打ちましょう。オプションはどんなipアドレスからの接続も受け付けますとかそんな意味だった気がします。
画面にjupyter notebookが起動され、tokenが表示されると思うのでこれをコピーしましょう。
ここでsdkのshellに戻って
gcloud compute ssh "インスタンス名" -- -N -L 28888:localhost:8888
と打ち込みます。
その後ブラウザのURL打つことろに「localhost:28888」と打ってアクセスします。
すると上みたいな画面になって、tokenを聞いてくるので上のやつを張り付けてゴールです。
入れたら色々importしてみて各種ライブラリが入っていることを確認してください。
終わりに
さっき成功して忘れないうちにかいてるので、もしかしたら上の通りにやってもだめかもしれません。
その時は教えてください。
あとkaggleにはkernelってやつがあって、notebook形式で人の成果を読むことができるすごいやつなんですが、なんと本当にnotebookのようにプログラムを実行できます。
参加しているコンペのページからNew kernelで作成すると訓練データなど一通り導入してある仮想環境が立ち上がります。
最初はここで遊ぶのが一番いいでしょう(無料だし、GPU使えるし)。ただ、外部からデータ持ってきたりとかその辺はいろいろできなかったりするので。
もっといい環境でやりたい場合に今回の方法がおすすめです。
公式imageはまだGPUをサポートしてないぽい?ですが、git読んでる感じそのうちリリースされそうなので待ちましょう。
ちなみに僕はこれに出ようかなぁと思ってます。なんか分子間のカップリングを予測するやつっぽいですね。
僕は物理科出身な上にこのあたりが割と近い専門なのですが、不勉強なので何のアドバンテージもありません。頑張ります。
www.kaggle.com
追記
kaggleを始めようぜって前提で記事書いたのに、データセット落とすとこ説明してませんでしたね。
kaggle APIを使いましょう、imageの中には導入されていなかったので以下に従って導入などを済ませてください。(僕はコンテナでやった)
qiita.com
基本この通りやればいいんですが、jsonファイルをアップするの面倒なんで~/.kaggleに入って、DLしたjsonの中身をコピペしましょう
echo "{\"username\":\"scibean\",\"key\":\"key\"}" > kaggle.jsonecho以下は中身のコピペで、"をバクスラでエスケープするのを忘れないでください。その結果をkaggle.jsonに書き込んでいます。
この設定が終われば後は自由に使えます。
画像のようにコンペのページに行くとdataタブの右下にapiでデータ落とす際のコマンドがあるのでコピペしましょう
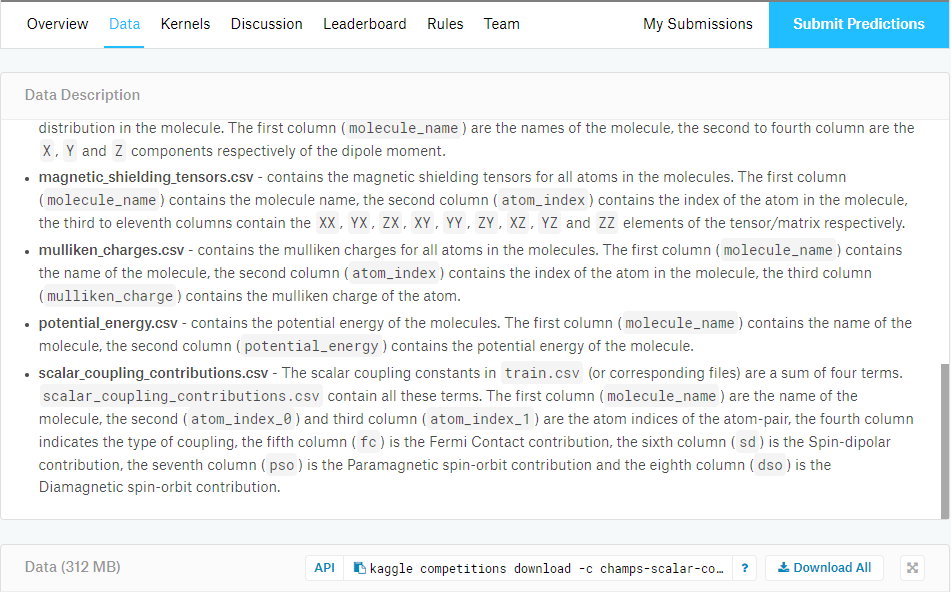
この時
mkdir data cd data
とやっておいてコピペしたコマンドに-wをつけるとカレントディレクトリにDLされます。
基本zipなのでunzipコマンドで解凍しましょう。
解凍先はなるべく指定した方がいいです。たまにファイル数がとんでもないやつがモリモリ出てきて大変なことになります(rm,mvコマンドにはファイル数に上限あるがので面倒なことになります)
では
VR、始めました。
最近VRを始めました。
VRreadyなPCを持っていたのでOculus RIFT Sを買ったんですがめちゃくちゃ満足してます。
身の回りにVRブームが来そうな機運を感じているので、今遊んでるソフトとかについて感想とか書いていきます。
VRchat

これはVtuber好きなら聞いたことあると思いますが、VR空間でアバターになりきってみんなとお話しするというプラットフォームです。
ロビーみたいな適当に集まった人がいる空間から、プライベートな空間まで色々で、すごく未来感がありました。
まずは、ロビーっぽいところ(Hubと呼ばれるワールド)へ行って、VRの民とコミュニケーションを図ります。

ロビーに先についていた友人(細身のロボット)ですが、いきなり外人に絡まれていました。
なんかでかいロボットのアバターに「zigzag zigzag oioioi」とひたすらに囁かれていたらしいです。
意味不明で恐怖していましたが、あとから調べると以下のような謎の動画が見つかったようです。
www.youtube.com
奥のかわいらしいアバターはスペイン人で、事あるごとに「North Korea is No1!!!!」と叫びまくる異常者でした。
友人も異常者なので事あるごとに鋭利な爪のアバターで目をつぶそうとしてきます。わかってても目がぞわぞわします。

BeatSaber

これも結構有名になってるんじゃないでしょうか。
音ゲーなんですが、曲に合わせて前からくる立方体を、手に持っている剣(モーションセンサ)で切るというやつです。
シンプルなんですが、VR感とうまくマッチしていて、良ゲーです。
多分今一番やってるのはこのゲームですね。曲と譜面を配布しているサイトもあるので最高です。
モーションセンサをブンブン振り回して、かがんだり移動したりする動作も要求されるので、思ったより運動になります。
プレイしていると汗だくになって、眼鏡がたまに曇るので、眼鏡ユーザーは対策した方がいいです。
DMMVRplayer、360度動画
言わずもがな、えちえちなやつです(360度動画は普通の動画がメイン)。非常に良いですね。
導入に手間取りましたが、大体提供元不明なアプリを許可でどうにかなるっぽいです。
これはDMMVRplayerでみたクマノミ天国

おわりに
紹介とかいってまだ全然遊べてないので、面白いの見つけ次第記事にしようかな。
今は勧められている東京クロノスが気になっています。
あとVRchatで使うためのアバターとHome空間を作成するために色々調べてます。
こちらもできたら記事にしたいね。